ПРИМЕНЕНИЕ ПЕРЕНОСА ЭЛЕМЕНТОВ В АНАЛИЗЕ И СИНТЕЗЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
К. С. Горшков, В. В. Филаретов
Введение. Преобразования электрических цепей называются
эквивалентными, если выполняется условие неизменности токов и
напряжений ветвей в тех частях схемы, которые не затронуты
преобразованиями [1, 2]. Эквивалентные преобразования электрических
цепей приводят к изменению конфигурации исходной схемы, при
сохранении ее характеристик.
Существует большое количество разнообразных преобразований
электрических цепей. Одним из наиболее наглядных видов эквивалентных
преобразований являются преобразования переносом элементов. Самыми
первыми нетривиальными преобразованиями стали преобразования
переносом источников эдс через сечение и источников тока по контуру
[1,2]. Эти преобразования вытекают из правил формирования уравнений
Кирхгофа. В данной статье исследуется история развития преобразований
переносом, которые были положены в основу эффективных методик
анализа [3–23] и синтеза электрических цепей [24–31].
Классические преобразования электрических цепей переносом
источников. Из уравнений Кирхгофа следует, что токи в электрической
цепи определяются заданными величинами суммарных эдс в контурах
независимо от того, из каких отдельных слагаемых они состоят. Поэтому
изменение расположения в схеме источников эдс, при котором суммарные
эдс во всех контурах сохраняются неизменными, не влияет на токи в
ветвях [2]. Аналогично, напряжения на ветвях определяются заданными
величинами суммарных токов источников тока в узлах, и поэтому
изменение в схеме расположения источников тока, при котором их
суммарные токи во всех узлах сохраняются неизменными, не влияет на
напряжения в схеме.
Следовательно, источник эдс может быть перенесен из какой-либо
ветви схемы во все другие ветви, присоединенные к узлу данной ветви, без
изменения токов в схеме. В дуальном случае, источник тока может быть
заменен источниками тока, подключенными параллельно всем ветвям,
которые составляли контур с рассматриваемым источником.
Как отмечено в учебнике [2, с. 68], «в ряде случаев в результате
переноса в схеме источников эдс или тока можно существенно облегчить
расчет электрической цепи», причем «перенос источников успешно
сочетается на практике с различными методами преобразований и
расчетов» (рис. 1).
Рис. 1. Классический перенос источников эдс и тока в учебнике [2]
В переводной работе [1, с. 123] предлагается «использование
преобразования переносом источника эдс через узел для уменьшения
числа узловых уравнений, подлежащих совместному решению».
Обобщение традиционных преобразований переносом. Несмотря
на то, преобразование переносом ветвей источников известно с середины
прошлого века, оно долгое время «не находило достаточно широкого
распространения» [3]. Причиной этому, по-видимому, являлась
«необходимость осуществлять дополнительные преобразования
источников тока в эквивалентные источники эдс и наоборот» [3, с. 1171].
Обратив внимание на эти обстоятельства, М.А. Шакиров предложил
правила переноса источников эдс по контуру и источников тока через узел,
целью которых было сделать метод переноса «удобным для практического
применения» [3, с. 1171].
Так, при переносе источника э.д.с. Ev из ветви с сопротивлением Zv в
другие, образующие с ней замкнутый контур, в k-ую ветвь этого контура
добавляется э.д.с., равная величине 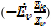 , совпадающая с направлением
обхода контура, выбранного по направлению э.д.с. Ev. , совпадающая с направлением
обхода контура, выбранного по направлению э.д.с. Ev.
На рис. 2 [3, c. 1172] показаны формальные этапы применения
правила преобразования переноса источника напряжения по контуру vpqst.
Рис. 2. Иллюстрация преобразования электрической цепи
переносом источника эдс Ev по контуру vpqst
При переносе источников э.д.с. через узел токи в ветвях, как показано
в [2], остаются неизменными, а напряжение между узлами изменяется на
величину перенесенной э.д.с. При переносе источников э.д.с. по контуру,
наоборот, остаются неизменными напряжения между узлами, а токи в
ветвях выделяемого контура изменяются на величину 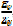 , где Ev
и Zv – параметры ветви, из которой произведен перенос э.д.с. В ветвях, которые
не были затронуты рассматриваемыми преобразованиями, остаются
неизменными как узловые напряжения, так и токи. , где Ev
и Zv – параметры ветви, из которой произведен перенос э.д.с. В ветвях, которые
не были затронуты рассматриваемыми преобразованиями, остаются
неизменными как узловые напряжения, так и токи.
Правило переноса источников тока по контуру формулируется в [3,
1172] следующим образом: при переносе источника тока Iv, имеющего
внутреннюю проводимость Yv, в другие ветви, присоединенные к узлу
этого источника, к k-му источнику тока узла добавляется источник тока Ikv,
равный величине 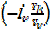 , имеющий такое же направление относительно
узла, как и источник Iv. , имеющий такое же направление относительно
узла, как и источник Iv.
Процесс преобразования схемы переносом источника тока через узел
иллюстрирует рис. 3. Отметим, что в оригинале в [3, с. 1172] в схеме на
рис. 3,г ошибочно изображено последовательное, вместо параллельного,
соединение четырех пар источников тока. Здесь представлен
исправленный вариант.
Рис. 3. Иллюстрация преобразования электрической цепи
переносом источника тока Iv через узел
При переносе источника тока через узел токи ветвей остаются
неизменными, а напряжение между узлами изменяется на величину Iv/Yv,
где Iv и Yv – параметры ветви, из которой произведен перенос источника
тока. В ветвях, которые не были затронуты рассматриваемыми
преобразованиями, остаются неизменными как узловые напряжения, так и
токи. Эквивалентность схем на рис. 2 и 3 следует понимать в смысле
неизменности токов, напряжений и мощностей во внешней электрической
цепи, ветви которой не преобразовывались.
Обобщенный в работе [3] класс преобразований переносом
источников позволяет в ряде случаев путем простых вычислений
существенно уменьшить число источников, действующих в схеме, что
может оказаться полезным при расчетах токов в ветвях, как в
установившемся режиме, так и в случае переходных процессов. С
помощью методов переноса источников можно получить преобразование
активной трехлучевой звезды в эквивалентный активный треугольник и
обратно. В работе [3] был, по-видимому, впервые продемонстрирован
перенос зависимых источников (управляемых ветвей). По этому поводу не
было сделано никаких комментариев, поскольку в уравнениях Кирхгофа
учет независимых и зависимых источников выполняется аналогично.
Публикация [3] стала началом глубоких исследований по изучению
свойств преобразования переносом и возможностей их применения для
решения таких задач теории цепей как схемный и диакоптический анализ,
а также структурный синтез.
Расширение правил преобразования переносом на двухполюсные
элементы. В 1975 году М.А.Шакиров обобщил преобразования переносом
на любые двухполюсные элементы. Так, при переносе проводимости вдоль
контура в ветви, образующие контур, добавляется переносимая
проводимость, которая имеет взаимную связь со всеми добавленными
проводимостями с коэффициентом взаимной связи по напряжению,
равным величине перенесенной проводимости, при одинаковой
маркировке их относительно контура; ветвь, из которой перенесена
проводимость, размыкается (рис. 4).
Рис. 4. Перенос проводимости g0 по контуру
При переносе сопротивления через узел (или сечение) в ветви,
сходящиеся к узлу (или сечению) добавляются взаимно связанные друг с
другом сопротивления, равные переносимому, с коэффициентом взаимной
связи по току, равного также переносимому сопротивлению, при
одинаковой маркировке их относительно узла; ветвь, из которой
перенесено сопротивление, заменяется идеальным проводником.
Перенос двухполюсных элементов стал возможным благодаря
использованию М.А. Шакировым не только классических правил
переноса, но и правил переноса ветвей напряжения (приемников
напряжения) (рис. 4) и ветвей тока (приемников тока), которые являются
управляющими ветвями зависимых источников. В отличие от правил
переноса источников эти правила можно считать обычным применением
второго и первого законов Кирхгофа.
Использование преобразований переносом элементов для анализа
линейных электрических цепей. Полный класс эквивалентных
преобразований электрических цепей переносом элементов,
исследованный в работах [3, 4], получил название переноса I рода.
Важнейшим свойством преобразований переноса I рода является принцип
независимости, позволяющий производить частичное упрощение схемы.
При этом весьма существенное значение имеют унаследованные
преобразованной путем переноса ветвей схемой начальные формы цепи –
остающиеся после переноса кондуктивные связи между оставшимися
ветвями исключенных у-контуров и соединенные друг с другом узлы
ветвей, на которые опирались исключенные z-сечения [15, 16].
Преобразования переноса I рода обладают свойством непрерывности
(поскольку допускают перенос любой части как активных, так и пассивных
элементов цепи) и являются средством для непрерывного преобразования
структуры схемы. Это позволяет использовать преобразования переноса I
рода для анализа электрических цепей [5, 6]. При этом важно, что
независимо от способа формирования система уравнений,
соответствующих методу контурных токов, отображает результат
преобразования z-схемы путем упрощения обобщенно-последовательных
соединений z-ветвей, а уравнения, соответствующие методу узловых
потенциалов, – результат преобразования схемы путем упрощения ее
обобщенно-параллельных соединений у-ветвей [13, 15, 16].
Применение правил переноса I рода совместно с преобразованиями
обращения ветвей позволяет осуществлять эквивалентные преобразования
электрических цепей, получившие название переноса II рода [7, 12, 14].
Перенос II рода является преобразованием, упрощающим обобщенно-
параллельно соединенные z-ветви и обобщенно-последовательно
соединенные у-ветви.
В отличии от обобщенных методов эквивалентных преобразований
электрических цепей, основанных на формальном отождествлении
матрично-алгебраических преобразований уравнений схем с исключением
их узлов или контуров, преобразования переноса I и II рода позволяют
представить преобразования схем как результат последовательного
изменения их структуры. Этот подход был положен в основу нового
направления в теории электрических цепей – схемоанализа [3–23].
На пути к синтезу. Одним из перспективных направлений в
структурном синтезе электрических цепей является генерация
(восстановление) схем, эквивалентных по символьной схемной функции
(ССФ), на основе порождающей схемы, полученной эвристическим путем
[32]. В этой связи был поставлен вопрос об использовании преобразований
переноса для структурного синтеза электрических цепей [24].
Рассматривались как классические преобразования [1, 2], так и
преобразования из схемоанализа или «общей теории схемных
преобразований» [15, 16, 18, 22]. Под переносом понимается
«исчезновение» элемента (путем нейтрализации стягиванием или
удалением) из одного места схемы и появление элементов с таким же
параметром в других местах схемы. Некоторые из новых элементов
объединяются с другими элементами соответствующих ветвей, что в
схемоанализе называется «растворением» элемента в других элементах.
Упрощение схемы (одним элементом меньше) достигается в случае,
если переносимый элемент растворяется в других элементах (что бывает
сравнительно редко). Но при этом параметр «исчезнувшего» элемента
будут нести другие элементы схемы, поэтому для структурного синтеза
такое преобразование не представляет интереса.
Преобразования переноса 1-го рода предусматривают перенос
элементов из ветвей дерева в хорды, что соответствует образованию
системы уравнений по методу контурных токов, или из хорд в ветви дерева
(для системы уравнений по методу узловых напряжений). Интересных для
практики структур при этом не образуется, поскольку появляются (в
изобилии) новые зависимые источники. Например, на рис. 4 вместо одной
проводимости мы получаем две проводимости и два источника тока,
управляемых напряжением.
Преобразования переноса 2-го рода по существу являются
вычислительной процедурой, имеют дело с одной и той же схемой,
параметры которой пересчитываются до получения решения. В результате
использования формул пересчета, содержащих операции умножения и
деления, параметры эквивалентных схем, получаемых методами переноса
2-го рода, отличаются от параметров порождающей схемы. На
промежуточных этапах также имеем дело со схемами, содержащими
большое количество зависимых источников.
Методы схемоанализа отличаются тем, что в них управляемые
источники изображаются в виде управляющих связей – стрелок
направленных от одной ветви к другой, а не в виде совокупности двух
элементов – управляемой управляющей ветви. Регулярность этой теории
преобразования обеспечивается рассмотрением переноса сопротивлений и
проводимостей, а многообразие положений активных элементов
оказывается за рамками теории. Перенос зависимых источников
ограничивается тривиальными частными случаями, когда несколько
источников с одинаковыми параметрами заменяются единственным
двухполюсником [22].
Раздельный перенос генераторов и приемников в теории схемоанализа
не предусматривается, а используется только на этапе вывода правил
переноса пассивных элементов (рис. 4) и не играет роли самостоятельного
преобразования. Если в получаемых схемах не сохраняется число
элементов (даже в простейших случаях), то новые схемы оказываются
неэквивалентными по символьным схемным функциям.
В процессе экспериментов с программой SymSyn [33],
предназначенной для восстановления полного множества схем, было
установлено, что в классе схем из двухполюсников не существует
неизоморфных схем, эквивалентных по ССФ. Поэтому перенос
двухполюсников не может привести к порождению новых структур, а
источником новых схемных решений являются активные элементы. В
дальнейшем нами был исследован раздельный перенос управляемых и
управляющих ветвей зависимых источников в дополнении к
классическому переносу ветвей независимых источников и откликов.
Строго говоря, до обсуждаемых ниже результатов использование
термина «перенос элемента» было не вполне корректным. Элемент не
переносился, а «размножался» и (частично) «растворялся». «Переносом»
было бы логичнее назвать такое преобразование, при котором один и тот
же элемент с одним и тем же параметром меняет положение
(переносится) из одного места схемы в другое.
Сохранение числа элементов при переносе генераторов и
приемников. Необходимым условием инвариантности к схемной функции
является сохранение числа элементов в схеме. Отметим, что применение
преобразования переносом элементов в общем случае приводит к
возникновению новых элементов [1, 2] или новых управляющих связей [4–
21], а значит изменяет символьную схемную функцию (ССФ)
преобразованных структур. В то же время существует принципиальная
возможность выполнения преобразования переносом активных элементов
при сохранении числа элементов, которая, по-видимому, впервые была
реализована в работе [3]. Переход от схемы на рис. 3,в к схеме на рис. 3,г
выполнен с помощью классического переноса независимого источника эдс
через узел, показанное на рис. 5. Как видно, в этом случае сохраняется
количество элементов, поскольку в одной из ветвей перенесенный
источник напряжения нейтрализуется источником тока.
Рис. 5. Перенос источника напряжения при сохранении числа элементов схемы
Таким образом, сохранение числа элементов при переносе источников
может быть обеспечено, если избыточные элементы порожденные в
результате эквивалентного преобразования схемы будут нейтрализованы.
В работах [24, 27] показано, что классическое правило переноса источника
эдс через узел и источника тока по контуру [1, 2] легко может быть
распространено на управляющие связи УИ и ветви откликов.
Следовательно, возможность сохранения числа элементов существует при
переносе всех типов ветвей активных элементов и искомых откликов.
Отметим, что для обсуждаемых частных случаев переноса активных
ветвей характерно отсутствие избыточных элементов и фактическое
перемещение на схеме одного и того же элемента, что позволило говорить
о новом преобразовании, получившим название «преобразование
переключением».
Условия выполнения преобразования переключением активных
ветвей. Для определения общих условий выполнения преобразований
переключением без изменения числа элементов использовался полный
класс правил нейтрализации активных элементов разработанных в рамках
метода схемных определителей [26], представленных в табл. 1. Здесь ветви
подразделяются на четыре типа: тип Е – независимые или управляемые
источники напряжения, тип J – независимые или управляемые источники
тока, тип U – искомые отклики напряжения или управляющие напряжения,
тип I – искомые отклики тока или управляющие токи.
Таблица 1. Условия нейтрализации ветвей активных элементов
Сохранение числа элементов при переключении активных ветвей,
оказывается возможным при выполнении ряда условий [24, 27],
представленных в табл. 2, которым должна удовлетворять порождающая
схема. Здесь элемент 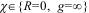 соответствует идеальному
проводнику, соответствует идеальному
проводнику, 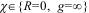 – разомкнутой ветви. – разомкнутой ветви.
Табл. 2. Условия выполнения переключения активных ветвей
Так, в примере на рис. 5 возможность переключения дуальных
источников определяет наличие в схеме сечения «b» (строка 1, табл. 2) и
контура «a»–«b»–«с»–«а» (строка 3, табл. 2). Как видно из этого примера, в
простейшем случае переключение дуальных активных ветвей в
соответствии с условиями табл. 2 через сечение и по контуру приводит к
одинаковому результату.
При переключении Е– или I–ветви (J– или U–ветви) через сечение
(контур) вместо нее помещается идеальный проводник (разомкнутая
ветвь), а сама переключаемая ветвь помещается последовательно
(параллельно) с 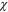 –ветвью. Следовательно, переключаемый элемент схемы
соединяется последовательно (параллельно) с единственным элементом,
который находится в рассматриваемом контуре или сечении, но не может
обеспечить нейтрализацию переключенного элемента. –ветвью. Следовательно, переключаемый элемент схемы
соединяется последовательно (параллельно) с единственным элементом,
который находится в рассматриваемом контуре или сечении, но не может
обеспечить нейтрализацию переключенного элемента.
Выполнение условий переключения обеспечивает применение
искусственного приема, предусматривающего введение короткозамкнутых
проводников 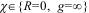 и разомкнутых ветвей и разомкнутых ветвей 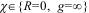 . При
этом если идеальный проводник можно создавать путем расщепления
произвольного сечения (узла), то разомкнутая ветвь может быть добавлена
в контур в виде фиктивной ветви, узлы которой не соединены элементами
схемы. . При
этом если идеальный проводник можно создавать путем расщепления
произвольного сечения (узла), то разомкнутая ветвь может быть добавлена
в контур в виде фиктивной ветви, узлы которой не соединены элементами
схемы.
Переключение Е–ветвей (I–ветвей) через сечение, включающее
дуальные J–ветви (U–ветви), может привести к тем же результатам, что и
переключение J–ветвей (U–ветвей) по контуру, включающему Е–ветви (I–
ветви). Поэтому, для получения полного множества схем с одинаковым
числом элементов с помощью переключения активных ветвей, необходимо
осуществлять проверку преобразованных структур на изоморфизм. Для
этого целесообразно использовать методику установления изоморфизма на
основе распределения показателей участия ветвей [25].
Свойства преобразования переключением активных ветвей.
Сохранение числа элементов – не единственное важное свойство
обсуждаемых преобразований. Так, в работе [28] установлено, что если
переключение не затрагивает ветви независимого источника и отклика, то
полученная схема будет инвариантна не только к передаточной
характеристике порождающей структуры, но и к ее входным/выходным
сопротивлениям.
В работе [29] исследовано влияние преобразования электрических
цепей переключением активных элементов на структуру эквивалентных
графовых моделей. Установлено, что условия выполнения переключения
совпадают с условиями построения графов, обуславливающими
инвариантность их структуры относительно данного вида преобразований.
Важно подчеркнуть, что обсуждаемые преобразования не имеют
ограничений на тип активных элементов и могут применяться как для схем
на традиционной аналоговой элементной базе – операционных усилителях,
повторителях тока и т.д., – так и для цепей на современных активных
компонентах, например, на транскондуктивных усилителях [29].
Существенно, что преобразование переключением позволяет
направленно модифицировать структуру в соответствии с критериями
технического задания [30], чтобы избежать необходимости анализа всех
возможных схемных вариантов. Так, в практических схемах используется,
как правило, подключение активных элементов к заземленному узлу.
Поэтому для получения патентоспособных схем требуется выполнять
перенос элементов относительно этого узла.
Анализ результатов экспериментов с программой SymSin,
представленные в работе [33], позволил установить, что: 1) синтез новых
эквивалентных схем возможен при наличии в порождающей схеме
дуальных по типу ветвей активных элементов и искомых откликов; 2) все
новые схемы получаются, минуя трудоемкий процесс восстановления, с
помощью преобразований переключением активных ветвей.
Для автоматизации получения множества схем, инвариантных по
ССФ, путем переключения ее активных элементов была разработана
компьютерная программа Switcher (авторы: О.А. Лагунков, А.С. Петров,
М.Ю. Разумков) [31]. В программе дополнительно реализована функция
выборки лучшего схемного решения по расположению узла с нулевым
потенциалом, а также по величине входного и выходного сопротивлений.
Перечисляем контура и сечения, удовлетворяющие условиям
сохранения. Сечение «3» включает генераторы K1 и В1 и единственный
элемент 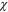 – управляющую ветвь В1 (строка 1, табл. 2). Сечение «2»
включает управляющие ветви K1 и В1 и единственный элемент – управляющую ветвь В1 (строка 1, табл. 2). Сечение «2»
включает управляющие ветви K1 и В1 и единственный элемент 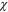 –
генератор В1 (строка 2, табл. 2). Контур «3»–«4»–«0»–«3» включает
генераторы K1 и В1 и фиктивную ветвь «0»–«4» (строка 3, табл. 2). Контур
«2»–«0»–«3»–«2» включает управляющие ветви K1 и В1 и фиктивную ветвь
«0»–«3» (строка 4, табл. 2). –
генератор В1 (строка 2, табл. 2). Контур «3»–«4»–«0»–«3» включает
генераторы K1 и В1 и фиктивную ветвь «0»–«4» (строка 3, табл. 2). Контур
«2»–«0»–«3»–«2» включает управляющие ветви K1 и В1 и фиктивную ветвь
«0»–«3» (строка 4, табл. 2).
Таким образом, множество сечений и контуров, удовлетворяющих
условиям сохранения будет состоять из сечений «2» и «3», а также
контуров «2»–«0»–«3»–«2» и «3»–«4»–«0»–«3». После выполнения
преобразования переносом активных элементов и исключения
изоморфных структур согласно алгоритму [27], получим схемы на рис. 6,б
и рис. 6,в. Отметим, что в результате переноса управляющих ветвей K1 и
В1 выход усилителя напряжения K1 замыкается на вход, что соответствует
замене K1 идеальным проводником, как показано на схеме на рис. 6,в.
Рис. 6. Получение технологичных схемных решений на основе порождающей схемы
операционного преобразователя (а) с помощью преобразования переносом
Как видно, исходная схема (рис. 6,а) не удовлетворяет требованию
технологичности, поскольку повторитель тока В1 не имеет общей точки с
источником сигнала и выходами усилителей K1 и K2. С помощью
предложенных преобразований удалось получить схемы на рис. 6,б и рис.
6,в, более технологичные, чем исходная, причем схема на рис. 6,в
содержит меньшее число активных элементов
Выводы: 1. Классические правила переноса источника напряжения
через сечение и источника тока по контуру, непосредственно вытекающие
из законов Кирхгофа, играли вспомогательную роль при анализе
электрических цепей [1, 2]. 2. Классические правила переноса были
дополнены М.А.Шакировым правилами переноса источника тока через
сечение и источника напряжения по контуру, а также правилами переноса
сопротивления по контуру и проводимости по сечению [3–19, 22, 23].
3. Перенос элементов не получил распространения в синтезе
электрических цепей, поскольку при переносе в общем случае происходит
усложнение схемы. Избежать увеличения числа элементов схемы позволил
учет условий взаимной нейтрализации дуальных элементов,
использованных ранее в рамках метода схемных определителей [26].
4. Преобразование электрических цепей переключением активных ветвей,
то есть переносом управляемого напряжения и управляющего тока через
сечение, а также переносом управляемого тока и управляющего
напряжения по контуру, совместно с условиями сохранения числа
элементов [26], является эффективным инструментом для порождения
полного класса эквивалентных схем с одинаковым числом элементов, что
важно при структурном синтезе и оптимизации электрических цепей [30].
1. Балабанян Н., Сешу С. Анализ линейных электрических цепей. –
М.: Госэнергоиздат, 1963. – 545 с.
2. Атабеков Г.И. Теоретические основы электротехники: в 3 т.– Т. 1.
Линейные электрические цепи.– М.:Энергия, 1966.– 320 с.
3. Шакиров М.А. Применение метода переноса источников для
расчёта и анализа линейных электрических цепей // Изв. вузов.
Электромеханика. – 1973. – №11. – С. 1171–1175.
4. Шакиров М.А. Перенос линейных пассивных элементов в
электрической цепи // Изв. вузов. Электромеханика. – 1975. – №5. – С.
449–452.
5. Шакиров М. А. Анализ линейной электрической цепи методами
переноса ее элементов // Электричество. – 1976. – №3.– С. 44–50.
6. Шакиров М. А. Составление уравнений электрической цепи в
однородных координатах методом последовательного переноса ее
элементов // Изв. вузов СССР. Электромеханика.– 1976.– №5.– С. 509–614.
7. Шакиров М. А. Алгоритм и программа анализа линейных
низкочастотных электронных схем методами переноса II рода на ЭВМ
«НАИРИ». Депонированная рукопись. – «Рипорт».– 1976.– №24.– 61 с.
8. Шакиров М. А. Алгоритм обращения ветвей линейной
электрической цепи // Изв. вузов СССР. Радиоэлектроника.– 1976.– Т. 19.–
№11.– С. 61–68.
9. Шакиров М. А. Формирование уравнений электрической цепи в
смешанных координатах методом последовательного переноса элементов
// Изв. вузов СССР. Радиоэлектроника.– 1976.– Т. 19.– №7.– С. 95–99.
10. Шакиров М.А. Эквивалентные преобразования схем с сечениями и
контурами // Изв. вузов СССР. Энергетика.– 1977.– Т. 1.– С. 117–119.
11. Шакиров М.А. Сокращение числа уравнений электрической цепи,
моделирующей линейные системы без управляющих связей.– Изв. вузов
СССР. Электромеханика.– 1977. – №2.– С. 173–177.
12. Шакиров М.А. Расчёт схемных функций и их чувствительности на
основе метода переноса II рода элементов линейной электрической цепи.–
Изв. АН СССР. Энергетика и транспорт.– 1977. – №2.– С. 91–99.
13. Шакиров М.А. Формирование узловых уравнений цепи методом
переноса I рода // Теоретическая электротехника.– Львов, 1978. – Вып.25. –
С. 59–63.
14. Шакиров М.А., Савинский П.Л. Новый метод расчёта узловых
напряжений линейной цепи преобразованиями переноса II рода //
Автоматизация проектирования в электронике. – Киев, 1978. – Вып. 18.
15. Шакиров М. А. Преобразования и диакоптика электрических
цепей. – Л.: Изд-во ЛГУ, 1980. – 196 с.
16. Шакиров М.А. Универсальные преобразования и диакоптика
электрических цепей: Автореф. дис. ... докт. техн. наук: 05.09.05 (Теорет.
основы электротехники) / Ленингр. политехн. ин-т.– Л.,1980.–32 с.
17. Шакиров М. А., Булавочкин В.П. Расчет нуллаторно-нораторных
y-схем по частям заменой y-подсхем z-радиальными эквивалентными
многомерными генераторами ЭДС // Электромеханика.–1984.–№ 8.–С.87–
91.
18. Шакиров М. А. Методы анализа сложных электрических цепей. –
Л.: ЛПИ, 1984.
19. Шакиров М.А. Расчет сложных z-схем методом преобразований
обобщенно-параллельных соединений: Методические указания.– Л.:
Ленингр. политехн. ин-т, 1985.– 28 с.
20. Булавочкин В. П. Многовариантный анализ и диакоптика
электрических цепей на основе методов обобщенных схемных
преобразований. Автореферат дис. … канд. техн. наук. – Л: Ленингр.
Политехн. ин-т им. М. И. Калинина, 1986. – 16 с.
21. Ермолаев Ю.В. Повышение точности анализа электрических цепей
на основе обобщенных преобразований их схем замещения при
выполнении многовариантных расчетов: Автореф. дис. ... канд. техн. наук:
05.09.05 (Теорет. электротехника) / Ленингр. гос. техн. ун-т.– Л., 1990.–
16 с.
22. Шакиров М. А. Теоретические основы электротехники : новые
идеи и принципы : схемоанализ и диакоптика. – СПб. : изд-во СПбГТУ,
2001. – 212 с.
23. Шакиров М.А. Перенос элементов электрической цепи через 2х2
полюсники // Электричество. – 2007. – №11.– С. 45–53.
24. Горшков К.С., Токарев Ю.В., Филаретов В.В. Эквивалентные
преобразования электрических цепей переносом управляющих ветвей //
Синтез, анализ и диагностика электронных цепей: Международный
сборник научных трудов / Под ред. В.В. Филаретова. – Ульяновск: УлГТУ,
2008. – Вып. 6.– C. 46–56.
25. Горшков К.С., Филаретов В.В. Установление изоморфизма
ненаправленных и ориентированных графов на основе распределения
показателей участия их ребер и дуг // Синтез, анализ и диагностика
электронных цепей: Международ. сб. науч. тр. – Ульяновск: УлГТУ, 2008.
– Вып. 6. – C. 56–72.
26. Горшков К. С., Токарев Ю. В., Филаретов В. В. Анализ и
структурный синтез электрических цепей методом схемных
определителей: учебное пособие.– Ульяновск: УлГТУ, 2008.– 240 с.
27. Горшков К.С., Филаретов В.В. Преобразование электрических
цепей переносом активных элементов через сечения и контуры с
нуллорами // Синтез, анализ и диагностика электронных цепей:
Международный сборник научных трудов / Под ред. В.В. Филаретова. –
Ульяновск: УлГТУ, 2009. – Вып. 7. – C. 38–45.
28. Горшков К.С., Филаретов В.В. Влияние преобразований
переключением активных элементов на входные и выходные
сопротивления цепи // Синтез, анализ и диагностика электронных цепей:
Международный сборник научных трудов / Под ред. В.В. Филаретова. –
Ульяновск: УлГТУ, 2009. – Вып. 7. – C. 30–37.
29. Горшков К.С. Порождение транскондуктивных реализаций
структурных схем электрических цепей преобразованием переключения //
Синтез, анализ и диагностика электронных цепей: Международный
сборник научных трудов / Под ред. В.В. Филаретова. – Ульяновск: УлГТУ,
2009. – Вып. 7. – C. 52–59.
30. Горшков К.С., Филаретов В.В. Структурная оптимизация
электронных схем переключением активных элементов // Электроника и
связь: Тематический выпуск «Электроника и нанотехнологии». – Киев,
2009.– С. 141–146.
31. Горшков К.С., Лагунков О.А., Петров А.С., Разумков М.Ю.
Switcher – программа структурного синтеза электрических цепей,
инвариантных относительно схемной функции.– М.: ОФЭРНиО
Госкоорцентра Минобрнауки России.–№ОФЭРНиО 00211; №ГР
50200900971.– 11.09.2009.
32. Волгин Л.И. Методы топологического преобразования
электрических цепей. – Саратов: Изд-во СГУ, 1982. – 108 с.
33. Горшков К.С., Токарев Ю.В. Реконструкция полных, цепных и
лестничных схем на основе формул схемных определителей // Схемно-
алгебраические модели активных электрических цепей Тр. международ.
конф. КЛИН–2007. – Ульяновск: УлГТУ, 2007. – Т. 3. – С. 39–48.
34. Волгин Л.И. Операционный преобразователь: Авторское
свидетельство №432524 (СССР). – Бюллетень изобретений, 1974.– №22.
Горшков Константин Сергеевич – к.т.н., старший преподаватель кафедры
«Электроснабжение» Ульяновского государственного технического
университета (УлГТУ); домашний адрес: г. Ульяновск, ул. Тельмана, д. 14, кв.
9; тел: (8908) 470-31-59; e-mail: K.Gorshkov@ulstu.ru.
Филаретов Владимир Валентинович – д.т.н., профессор кафедры
«Электроснабжение» Ульяновского государственного технического
университета (УлГТУ); e-mail: vvfil@mail.ru
|

