Число слагаемых в нуллорно-весовых выражениях сокращается, если использовать неравновесные нуллорные схемы, содержащие различное число нораторов и нуллаторов [98]. Число неравновесных нуллорных схем меньше числа соответствующих равновесных нуллорных схем – содержащих одинаковое число нораторов и нуллаторов. Число базисных неравновесных нуллорных схем, в которых нораторов больше (меньше) нуллаторов на единицу, приведено в строке 7 табл. 1. Для трехполюсной подсхемы все 6 неравновесных базисных НС приведены в табл. 7. Правила эквивалентности при построении базисных неравновесных нуллорных схем такие же, как и для базисных равновесных НС – содержащих одинаковое число нуллаторов и нораторов.
Неравновесными НС характеризуются подсхемы, в которых число приемников не равно числу генераторов управляемых источников (УИ). Поэтому при анализе схема может быть разделена на подсхемы, имеющие управляющие связи между собой.
Нуллорные схемы для автономных подсхем [102]. Сократить число нуллорных схем можно также путем использования автономных вместо общепринятых неавтономных подсхем. Множество нуллорных схем автономной подсхемы содержит как равновесные, так и неравновесные нуллорные схемы. Они необходимы, поскольку при использовании автономных подсхем требуется информация как о составляющих числителя, так и составляющих знаменателя. Здесь в отличие от объединения на основе неавтономных многополюсников нет отдельных операций объединения с нуллорными схемами числителя и знаменателя для получения выражений для числителя и знаменателя соответственно.
Равновесные нуллорные схемы получаются путем выделения всех элементов из подсхемы при нейтрализованных независимых источниках (НИ), а неравновесные нуллорные схемы – из подсхемы числителя [91], содержащей НИ. Получающиеся при этом НС являются неравновесными, поскольку при выделении НИ появляется направленный норатор, а соответствующий ему нуллатор находится в другой подсхеме. При этом число нораторов в неравновесных нуллорных схемах для подсхемы, содержащей НИ и не содержащей приемник отклика, будет на единицу больше числа нуллаторов. Общее число нуллорных схем автономной подсхемы (строка 8 табл. 1) находится как сумма числа равновесных и неравновесных НС. Для трехполюсной подсхемы все 17 базисных НС автономной подсхемы получаются путем объединения НС в табл. 6 и 7.
Как видно из табл. 1 число базисных НС автономной подсхемы в 5…10 раз меньше числа базисных НС соответствующей неавтономной подсхемы, число полюсов которой на минимальное число – единицу (полюс независимого источника) больше числа полюсов автономной подсхемы. Во столько же раз уменьшаются затраты при объединении подсхем, одна из которых является автономной. Выигрыш увеличивается при большем числе независимых источников.
Иллюстрация метода объединения подсхем на основе нуллорных схем. Для сравнения с методом d-деревьев приведем решение изложенной выше задачи методом НС. При этом нуллорно-весовое выражение для транзистора формируется методом выделения параметров [89]
Схемы под знаком определителя – базисные НС. Нумерация полюсов на этих схемах проведена в соответствии с рис 1,б.
Для пассивной подсхемы нуллорно-весовое выражение находится путем последовательного выделения проводимостей (нумерация полюсов в нуллорных схемах соответствует рис. 1,в):
где весовые коэффициенты нуллорных схем
Из (15) видно, что подсхема имеет 10 базисных НС из 87-ми (строка 5
табл. 1). Причем в этой формуле весовые коэффициенты получены в
свернутом компактном виде, в отличие от соответствующих
коэффициентов по методу d-деревьев (табл. 4), что достигнуто
использованием формулы выделения проводимости (12).
Объединение подсхем проиллюстрировано в табл. 8. Нуллорные
схемы для активной и пассивной подсхем представлены в первой строке и
первом столбце соответственно. При объединении НС получается 50
объединенных схем. Из них нуллорными схемами объединенной подсхемы
являются только 38 схем, которые после их эквивалентного
преобразования к базисным НС, представлены в табл. 8. Остальные 12
схем вырождены и поэтому не приводятся.
Из 38-ми НС в табл. 8 различными являются только 20 схем. Их
номера проставлены в правом верхнем углу ячеек. Отметим, что НС с
номерами 1…10 уже использовались для описания пассивной подсхемы.
12 НС с номером 1 и их весовые коэффициенты составляют определитель
схемы. Эти НС можно представить (по аналогии с объединенными d-
деревьями в (9)) парами чисел, обозначающими в табл. 8 порядковые
номера соответствующих НС активной и пассивной подсхем:
Символьное выражение определителя находится путем перемножения
пар весовых коэффициентов нуллорных схем с номерами из формулы (16).
С учетом группировки слагаемых получаем
Как видно из (17), метод НС в отличие от метода d-деревьев не
образует взаимно уничтожающихся слагаемых, поскольку он не
использует избыточной унисторной схемы УИ, а базируется
непосредственно на схеме замещения цепи, где каждый элемент
встречается только один раз. При этом снижается трудоемкость
построения структурно-весовых выражений исходных объединенных
подсхем – требуются только 50 операций объединения НС вместо 108
операций объединения d-деревьев.
Анализ схемы активного полосового фильтра [64, 85, 94]
(в решении принимал участие Ф.А.Королев). Полосовой фильтр
представлен на рис. 2.
Подсхема 1 дана на рис. 3,а. Подсхемы 2–4 отличаются от подсхемы 1
только обозначениями элементов. Порядковые номера резисторов и
конденсаторов подсхем 2–4 вычисляются через номера элементов
подсхемы 1 по формулам:
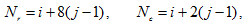 |
(18) |
где i – номер параметра в подсхеме 1; j – номер одной из подсхем 2–4.
Подсхема 5 изображена на рис. 3,б. Дерево объединения подсхем
представлено на рис. 3,в.
Нахождение нуллорных инвариантов подсхем полосового
фильтра. Для обозначения коэффициентов нуллорных схем используется
символ «Х» с двумя цифрами: верхний индекс – номер подсхемы, а
нижний – порядковый номер нуллорной схемы. Коэффициенты
X21, X22, X23, X31, X32, X33, X41, X42, X43
определяются на основе X11, X12, X13 соответственно с помощью формул (18).
В результате выделения элементов получаются следующие
инварианты подсхем:
Объединение нуллорных инвариантов подсхем полосового
фильтра. Выполняется согласно иерархическому дереву на рис. 3,в.
Номера узлов этого дерева соответствуют номерам исходных подсхем
(подсхемы 1–5) и подсхем, образованных в результате объединения
(подсхемы 6–9). В табл. 9 представлен процесс объединения подсхем 1 и 2.
Здесь белым кружком показан узел, который будет отсутствовать в
объединенной подсхеме – внутренний узел.
После приведения подобных слагаемых по табл. 9, учета тождеств
[91] получаем нуллорный инвариант подсхемы 6
В табл. 10 представлено объединение подсхем 5 и 8. Полученная
подсхема с номером 9 завершает процесс объединения и является
исходной схемой.
После приведения подобных слагаемых в табл. 9 и учета схемно-
алгебраических тождеств [91] получаем нуллорный инвариант исходной
схемы
При нахождении коэффициента передачи активного полосового
фильтра необходимо объединить подсхему 9 с норатором на входе и
нуллатором на выходе (для числителя), а также с идеальным проводником
на входе (для знаменателя) [94]. Отсюда
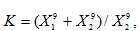 |
(23) |
что соответствует результам [64, 85, 94].
Необходимо отметить, что число подформул в решении сокращено с
35 (метод базисных нуллорных схем [94]) до 26, как в методе двоичных
векторов [85]. Кроме того, формула по предлагаемому методу требует
меньшее количество объединений – два вместо четырех (в методе
базисных нуллорных схем), а, следовательно, обеспечивает значительное
сокращение времени и трудоемкости анализа. Следует отметить, что
решение, данное в [85], практически не может быть повторено другими
специалистами из-за сложной алгебраической процедуры нахождения
знаков при объединении подсхем.
Метод нуллорных схем реализован В.В.Филаретовым в компьютерной
программе CIRTRE. Для задания последовательности объединения
подсхем в программе CIRTRE предусматривается использование
модифицированного cir-файла, в котором отображается иерархия
вложения подсхем до образования исходной схемы. Объединение двух
подсхем задается двуми строками строкой «X<номер промежуточной
подсхемы> <множество внешних узлов>» и строкой «.X». Эти строки в
отличие от аналогичных строк, обрамляющих в cir-файле строки,
относящиеся к элементам исходных (терминальных) подсхем, указывают
на формирование промежуточных подсхем (включая исходную схему),
которых на единицу меньше числа исходных подсхем. Важно, что
модифицированный таким образом cir-файл по существу является
программой, задающей порядок объединения подсхем.
Анализ схемы операционного усилителя ?A741. 76-узловая схема
замещения этого усилителя включает 115 резисторов, 76 конденсаторов и
26 ИТУН (рис. 4) [103]. Схема разделена на 26 подсхем пунктиром, их
номера соответствуют обозначениям элементов подсхемы.
На рис. 6 рассмотрены три варианта объединения подсхем: на рис. 6,а
– последовательное объединение, на рис. 6,б – иерархическое
объединение, состоящее из двух неравных (по количеству подсхем) частей
и на рис. 6,в – иерархическое объединение, состоящее из двух равных
частей.
Количество получаемых нуллорных и базисных нуллорных схем, показатели сложности формируемых выражений для рассматриваемых трех вариантов объединения (рис. 5) через запятые приведены в табл. 10 соответственно. В первом столбце указаны порядковые номера подсхем, которые требуются для работы программы CIRTRE, которая нумерует подсхемы в порядке следования в cir-файле [94], а в скобках – номера подсхем в соответствии с рис. 4. В последней строке табл. 10 приводится суммарное количество нуллорных и базисных нуллорных схем, умножений, сложений и вычитаний в выражениях, образующих соответствующие последовательные формулы.
Как видно, в зависимости от вида объединяемых подсхем число используемых базисных схем намного меньше числа нуллорных схем (включающего базисные схемы). Предпочтительным вариантом является иерархическая «сборка» схемы с ее входа и выхода так, чтобы две промежуточные подсхемы, образующие исходную схемы были примерно одинаковой сложности.
Символьные выражения искомых коэффициентов передачи, которые выдает программа CIRTRE, могут содержать избыточные символы и операции (например «*1», «*(1)»). Для дополнительного редактирования алгебраических выражений коэффициентов передачи используется программа LIKVID [93].
Анализ операционного усилителя ?A741 проводился на персональном компьютере Intel Pentium D 930 с тактовой частотой процессора 3 ГГц и оперативной памятью 2 Гб. Показатели сложности символьной функции для передаточного коэффициента по напряжению для различных вариантов объединения подсхем (рис. 5,а–в) приведены в табл. 12. При подсчете числа операций учтено (для подсхемы 51), что в передаточной функции используется только часть базисных схем с ненулевыми коэффициентами.
Как видно из табл. 12, наиболее эффективным оказалось объединение подсхем по дереву на рис. 5,в. При этом еще раз проиллюстрировано [91], что следование принципу половинного деления в символьной диакоптике [77] обеспечивает формирование минимальных по сложности выражений.
Избирательный усилитель [38, 94]. Схема представлена на рис. 1, где она разделена на девять подсхем, номера которых помечены курсивом. Дерево объединения подсхем, которое использует программа CIRTRE, показано на рис. 6. Число нуллорных и базисных нуллорных схем дано в третьем и четвертом столбцах табл. 13 соответственно. Как видно, число используемых базисных нуллорных схем может быть меньше общего числа нуллорных схем, получаемых при формировании САФ, более чем в 1000 раз.
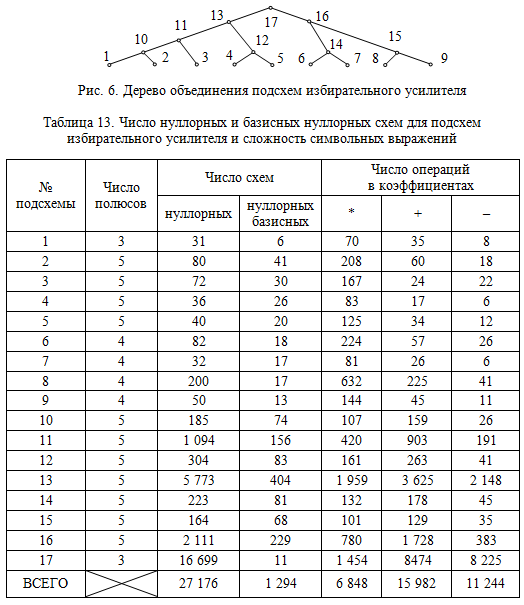 |
Полученная за 7.77 секунды (Pentium-4; 2 ГГц) символьная функция для передаточного коэффициента по напряжению содержит 1289 подвыражений, 6180 умножений, 11535 сложений и 6621 вычитание. Здесь учтено, что в передаточной функции присутствует только 6 из 11-ти базисных нуллорных схем подсхемы 17 (исходной схемы). Это сокращает число умножений более, чем на 10 %, а число аддитивных операций – на треть. Результаты получены при первоначальном выделении пассивных элементов. При преимущественном выделении активных элементов число умножений увеличивается приблизительно на 3%, а остальные характеристики практически не изменяются.
Выводы
1. Метод d-деревьев предназначен для иерархического анализа цепей, представленных унисторными y-графами. D-деревья подсхем формируются с помощью трудоемких алгоритмов поиска путей в подграфе. При анализе активных цепей образуются взаимно уничтожающиеся слагаемые как на этапе анализа подсхем, так и при их объединении.
2. Метод объединения подсхем на основе нуллорных схем позволяет анализировать схемы с произвольными линейными элементами. Электрическая цепь может быть задана ее нуллорными схемами, образующими нуллорный инвариант: пассивный, базисный, минимизированный базисный или матричный. Нуллорный инвариант объединенной схемы получается как декартово произведение инвариантов подсхем. Схемно-алгебраические тождества позволяют уменьшить и минимизировать число нуллорных схем, входящих в инвариант.
3. Метод нуллорных схем позволяет анализировать электрические цепи с любым числом независимых источников непосредственно – без использования традиционного метода наложения. Для этого используются нуллорные схемы автономных подсхем, которых значительно меньше, чем нуллорных схем соответствующих неавтономных подсхем. Поэтому применение нуллорных схем автономных подсхем сокращает многократно число теретико-множественных операций формирования символьных выражений откликов.
4. Матричные операции удаления-объединения строк и столбцов приводят к формированию избыточных выражений при анализе электрических цепей по частям. Схемно-топологический метод нуллорных схем позволяет избежать образования взаимно уничтожающихся слагаемых, как при анализе подсхем, так и при их объединении, не требует нахождения знаков, использует единую процедуру анализа начальных подсхем и их объединения, обеспечивает получение более компактных выражений с меньшей трудоемкостью.
5. Алгоритмы формирования схемно-алгебраических формул определителя (нуллорных схем с коэффициентами) и иерархического объединения подсхем, реализованы в компьютерной программе CIRTRE для получения символьных выражений, содержащих информацию обо всех схемных функциях заданной цепи. Программа CIRTRE использует модифицированный cir-файл, который является, в свою очередь, программой, задающей порядок объединения подсхем.
Литература
1. Kirchhoff G. Uber die Auflosung der Gleichungen auf welche man bei der Untersuchung der linearen Verteilung galvanischer Strome gefuhrt wird // Annalen der Physik und Chemie.– 1847.– Bd. 11.– S. 497–508.
2. Кирхгоф Г.Р. Избранные труды.– М.: Наука, 1988.– 428 с.
3. Maxwell J.C. Chap. 6 and appendix // Electricity and magnetism. 1.– Oxford: Clarendon press.– 1892.– P. 403–410.
4. Максвелл Д.К. Трактат об электричестве и магнетизме. В 2-х т. Т. 1.– М.: Наука, 1989.– 416 с.
5. Feussner W. Ueber Stromverzweigung in netzformigen Leitern // Annalen der Physik.– 1902.– Bd 9, N 13.– S. 1304–1329.
6. Филаретов В.В. Исследования Вильгельма Фойснера в области теоретической электротехники // Электричество.– 1992.– № 9.– С. 64–67.
7. Крон Г. Исследование сложных систем по частям – диакоптика. – М.: Наука, 1972. – 544 c.
8. Percival W.S. Solution of passive electrical networks by means of mathematical trees.– London: Inst. Electr.Engrs.– Part 3.– 1953.– P. 143–150.
9. Percival W.S. Improved matrix and determinant methods for solving networks // Digests of institution monographs.– 1954.– Monograph No. 96 (Radio section).– P. 278–279.
10. Percival W.S. The graphs of active networks // Digests of institution monographs.– Monograph No. 129 (Radio section).–1954.– P. 727–729.
11. Bott R., Mayberry I.P. Matrices and trees // Economic activity analysis.– New York, 1954.
12. Boisvert M., Robichoud L.P.A. Analyse directe des reseaux electriques // Rapport de Recherches / Dept. du genie electrique, Universite Laval.– 1956.– N 9.
13. Mason S.J. Topological analysis of linear non-reciprocal networks // Proc. IRE (Institute of Radio engineers, Institute of Electrical and Electronics Engineers – IEEE с 1963 г.).– 1957.– Vol. 45, N 6.– P. 829–838.
14. Галямичев Ю.П. Топологический метод анализа линейных электрических схем // Науч.– техн. сб. Госкомитета Совета Министров СССР по радиоэлектронике.– 1958.– Вып. 2.– С. 66–76.
15. Галямичев Ю.П. Топологический метод анализа линейных электрических схем: Автореф. дис. ... канд. техн. наук / Ленингр. ин-т инженеров жел.–дор. транспорта.– Л., 1959.– 13 с.
16. Галямичев Ю.П. Расчет активных схем при помощи деревьев схем // Электросвязь.– 1960.– № 8.– С. 48–57.
17. Мэзон С., Циммерман Г. Электронные цепи, сигналы и системы.– М.: Изд-во иностр. лит., 1963.– 620 с.
18. Робишо Л., Буавер М., Робер М. Направленные графы и их приложение к электрическим цепям и машинам.– М.–Л.:Энергия, 1964.– 248 с.
19. Chen W.K. Topological analysis for active networks // IEEE Trans. On circuit theory.– 1965.– Vol. CT–12, N 1.– P. 85–91.
20. Блажкевич Б.И. Применение топологических методов к исследованию линейных систем // Теоретическая электротехника.– Львов, 1966.– Вып. 1.
21. Максимович Н.Г. Применение множеств для анализа и расчета сложных цепей // Теоретическая электротехника.– Львов, 1966.– Вып. 1.– С. 50–58.
22. Калниболотский Ю.М. Анализ линейных электронных схем методом выделения несимметричной части определителя матрицы схемы // Изв. сузов СССР. Радиоэлектроника.– 1967.– Т. 10, № 7.– С. 641–650.
23. Блажкевич Б.И. Определение передачи линейной цепи с помощью прадеревьев графа проводимостей // Теоретическая электротехника.– Львов, 1967.– Вып. 3.– С. 111–119.
24. Сигорский В.П., Калниболотский Ю.М. Алгоритмы анализа электронных схем // Изв. вузов. Радиоэлектроника. – 1968. – Т. 11, № 11.– С. 1125–1145.
25. Дмитришин Р.В. Расч?т линейных цепей методом расширенных структурных чисел // Изв. вузов СССР. Радиоэлектроника. – 1969. – Т. 12, № 8. – С. 806–813.
26. Калниболотский Ю.М., Рысин В.С. Топологический анализ электронных схем // Радиотехника.– 1969.– Т. 24, № 4.– С. 30–34.
27. Максимович Н.Г. Методы топологического анализа электрических цепей.– Львов: Изд. Львов. ун-та.– 1970.– 257 с.
28. Блажкевич Б.И. Топологические методы анализа электрических цепей и перспективы их развития // Отбор и передача информации.– Киев, 1970.– Вып. 26.– С. 20–34.
29. Гарибян Р.М. Топологический метод разложения графа сети на части // Изв. вузов СССР. Энергетика.– 1970.– № 8.– С. 7–10.
30. Сешу С., Рид М.Б. Линейные графы и электрические цепи.– М.: Высш. шк., 1971.– 448 с.
31. Chen W.K. Applied graph theory.– Amsterdam–London: North-Holland publishing company, 1971.– 484 s.
32. Беллерт С., Возняцки Г. Анализ и синтез электрических цепей методом структурных чисел. – M.: Мир, 1972. – 334 c.
33. Дмитришин Р.В. Алгоритмы символического определения схемных функций линейных цепей на ЭВМ (метод расширенных структурных чисел и его реализация): Дис. … канд. техн. наук № 276 (Теоретические основы электротехники) / Львов. политехн. ин-т.– Львов, 1972.– 164 с.
34. Матвийчук Я.Н. Топологический метод определения характеристического полинома электронной схемы по частям // Теоретическая электротехника и машинное проектирование электронных цепей.– Киев, 1973.– С. 192–200.
35. Дмитришин Р.В., Шаповалов Ю.И. Об одном алгоритме нахождения параметров линейных радиосхем на ЭВМ // Всесоюзная конф. «Современные методы и аппаратура для измерения параметров радиотехнических цепей».– Новосибирск: Сибирский науч. исследовательский ин-т метрологии, 1973.– С. 30–33.
36. Анисимов В.И., Козьмин Н.Г. Анализ электронных схем на ЭЦВМ методом k-деревьев // Изв. вузов. Радиоэлектроника, 1973, № 6.– С. 54–59.
37. Анисимов В.И., Козьмин Н.Г. Анализ электронных схем на ЭЦВМ обобщенным методом K-деревьев // Изв. вузов. Радиоэлектроника, 1973, № 11.– С. 75–78.
38. Лаксберг Э.А. Частотный анализ линейных электронных схем с помощью ЭЦВМ на основе y-матрицы // Автоматизация проектирования в электронике.– Киев, 1973.– Вып. 8.– С. 22–32.
39. Матвийчук Я.Н. Разработка и реализация на ЭВМ некоторых алгоритмов топологического анализа электронных схем: Дис. … канд. техн. наук: 05.09.05 (Теоретические основы электротехники) / Львов. политехн. ин-т.– 1974.– 190.
40. Блажкевич Б.И., Комиссарчук А.А., Мочернюк Ю.П. Поиск суммы прадеревьев графа проводимостей при расщеплении цепи на две подсхемы // Электричество.– 1974.– № 9.– С. 85–87.
41. Дмитришин Р.В., Шаповалов Ю.И. Диакоптический алгоритм анализа сложных линейных цепей на ЭВМ // Автоматизация проектирования в электронике. – Киев: Техника, 1975. – Вып. 12. – С. 42–46.
42. Konczykowska A. Zastosovanie metod dekompozycji do analizy ukladow elektrycznych // Wydawnictwa Politechniki Warzawskiey: Prace naukowe. Electronica.– 1975.– Nr. 20.
43. Дмитришин Р.В., Шаповалов Ю.I. Алгоритм кодувания та зведения пiдсхем при моделюваннi складнiх радiосхем // Вiсник Львiвського полiтехнiчного iн-ту: Радiоелектроннi мережiта та пристрої.– Львiв: Вища школа, 1976.– № 103.– С. 118–120.
44. Блажкевич Б.И., Мочернюк Ю.П. Топологический анализ сложных графов методом наращивания // Теоретическая электротехника.– Львов, 1976.– Вып. 20.– С. 23–27.
45. Козьмин Н.Г. О топологическом расчете сложных электронных схем делением их на части // Изв. Ленингр. электротехн. ин-та.– 1976.– Вып. 195.
46. Блажкевич Б.И., Мочернюк Ю.П. Топологический анализ графа цепи методом наращивания при расщеплении графа на элементарные подграфы // Отбор и передача информации.– Киев, 1977.– Вып. 50.– С. 49–55.
47. Блажкевич Б.И., Мочернюк Ю.П. Метод системных графов и его применение для анализа линейных систем / Физ.– мех. ин-т АН УССР.– Препринт № 2.– Львов, 1977.– 56 с.
48. Дмитришин Р.В., Шаповалов Ю.И. Вычисление схемных функций при многовариантном анализе схем // Изв. вузов СССР. Радиоэлектроника.– 1978.– Т. 21, № 6.– С. 151–153.
49. Шаповалов Ю.И. Машинный топологический расчет схемных функций электронных схем методом подсхем. Дис. … канд. техн. наук: 05.13.12 (Системы автоматизированного проектирования и автоматизация технологической подготовки производста в электронной и электротехнической промышленности) / Львов. политехн. ин-т.– Львов.– 1978.– 165 с.
50. Машинная оптимизация электронных узлов РЭА / А.Г.Ларин, Д.И.Томашевский, Ю.М.Шумков, В.М.Эйдельнант.– М.: Сов. Радио, 1978.– 192 с.
51. Березко Л.А., Шаповалов Ю.И. Реализация метода подсхем при символическом анализе линейных схем // Изв. вузов СССР. Радиоэлектроника.– 1980.– Т. 23, № 6.– С. 21–25.
52. Матвийчук Я.Н. Разработка метода и программы анализа линейных схем по частям // Теоретическая электротехника.– Львов, 1980.– Вып. 29.– С. 41–52.
53. Дмитришин Р.В. Оптимизация электронных схем на ЭВМ.– К.: Техника, 1980.– 224 с.
54. Starzyk J., Sliwa E. Hierarchic decomposition method for the topological analysis of electronic networks // Circuits theory and applications, 1980, vol. 8.– P. 407–417.
55. Воробкевич А.Ю., Мочернюк Ю.П., Шегедин А.И. Программа анализа сложных электрических цепей по частям // Машинное проектирование электрических и электронных цепей.– Киев, 1981.– С. 30–35.
56. Starzyk J. Analisa topologiczna duzych ucladow electronicznych// Electronika.– Warszawa: Prace naukove politechniki warshawskiej. –1981.– N 55.– P. 131–175.
57. Ястребов Н.И. Способ кодирования обобщенного числа при использовании декомпозиционного метода раскрытия определителя // Изв. вузов СССР. Радиоэлектроника, 1982.– Т. 25, № 6.– С. 83–85.
58. Ланнэ А.А., Михайлова Е.Д., Саркисян Б.С., Матвийчук Я.Н. Оптимальная реализация линейных электронных RLC-схем.– Киев: Наук. думка, 1982.– 208 с.
59. Шаповалов Ю.И., Давидюк Р.Д. Особенности реализации метода топологического анализа схем в программе АС13ЕС // Изв. вузов СССР. Радиоэлектроника, 1983.– Т. 26, № 6.– С. 79–81.
60. Konczykowska A., Wojciechowski J. Podstawy topologicznych metod analizy ukladow elektrycznych.– Warszawa–Wroclaw: Panstwowe wydawnictwo naukowe, 1983.– 254 s.
61. Starzyk J., Sliwa E. Upward topological analysis of large circuits using directed graph representation // IEEE Transactions on circuits and systems.– 1984.– N 4.– P. 410–414.
62. Дмитришин Р.В. Генерация схемных функций методом буквенно-полиномиальной редукции // Электронное моделирование.– Киев, 1985.– Т. 7, № 1.– С. 36–40.
63. Ястребов Н.И. Повышение эффективности декомпозиционных алгоритмов символьного анализа // Радиоэлектроника.– 1985.– № 6.– С. 102–104.
64. Starzyk J. A., Konczykowska A. Flowgraph analysis of large electronic networks // IEEE Transactions on circuits and systems. – 1986. – Vol. CAS–33, N 3. – P. 302–315.
65. Wojciechowski J. Topologiczna analiza sieci elektrycznych z wykorzystaniem dekompozycji. 1. Analiza ukladu zdezomponowanego // Archiwum elektrotechniki.– 1986.– T. 23, z. 4.– S. 601– 610.
66. Wojciechowski J. Topologiczna analiza sieci elektrycznych z wykorzystaniem dekompozycji. 2. Dekompozycja bez defectu // Ibid.– S. 611– 624.
67. Рыбин А.И., Скрынский В.С., Шарпан О.Б., Ястребов Н.И. Методические указания к выполнению расчетно-графической работы по основам теории цепей.– Киев: КПИ, 1987.– 44 с.
68. Филаретов В.В. Алгоритмы символьно-топологического анализа электрических цепей: Дис. ... канд. техн. наук: 05.09.05 (Теорет. электротехника) / Ленингр. гос. техн. ун-т.– Л., 1990.– 148 с.
69. Филаретов В.В. Программа SYMBOL автоматического вывода передаточной функции электронной схемы произвольной структуры // Алгоритмы и устройства обработки сигналов и автоматизация проектирования.– Таллин: АН Эстонии, 1991.– С. 130–148.
70. Филаретов В.В. Алгоритм приведения развернутых алгебраических выражений топологических функций к скобочной форме и его реализация в программе SYMBOL // Алгоритмы и устройства обработки сигналов и автоматизация проектирования.– Таллин: АН Эстонии, 1991.– С. 149–166.
71. Филаретов В.В. Топологический анализ электронных схем методом выделения ветвей и дуг // Электричество.– 1992.– № 7.– С. 31–37.
72. Филаретов В.В. Обобщенный унисторный граф электронной схемы и его анализ // Электричество.– 1993.– № 5.– С. 65–70.
73. Филаретов В.В. Оптимизация формул схемных функций электрических цепей // Электричество.– 1993.– № 9.– С. 64–68.
74. Филаретов В.В., Шеин Д.В. Адаптивный алгоритм и программа генерации сверхкомпактных символьных выражений схемных функций // Проблемы автоматизированного моделирования в электронике: Тез. докл. международ. конф.– Киев: Об-во “Знание” Украины, 1993.– С. 28–29.
75. Филаретов В.В., Шеин Д.В. Машинная генерация оптимальных формул для функций пассивных схем // Проблемы автоматизированного моделирования в электронике: Сб. докл. международ. конф.– Киев: Политехн. ин-т, 1994.– С. 28–32.
76. Филаретов В.В., Шеин Д.В. Оптимальный синтез символьных функций для сложных схем с операционными усилителями // Проблемы физической и биомедицинской электроники: Сб. докл. международ. конф.– Киев: Политехн. ин-т, 1995.– С. 216–220.
77. Филаретов В.В. Синтез оптимальных формул схемных функций электрических цепей // Электричество.– 1995.– № 4.– С. 36–43.
78. Дмитришин Р.В. Полиномиальные методы символьного анализа электрических цепей: Дис. ... докт. техн. наук: 05.09.05 (Теорет. электротехника) / Гос. ун-т «Львовская политехника».– Львов, 1996.– 284 с. (На укр. языке).
79. Филаретов В.В. Об иерархическом подходе к символьному анализу сложных электронных схем // Проблемы физической и биомедицинской электроники: Сб. докл. международ. конф.– Киев: Национальный техн. ун-т Украины, 1996.– С. 132–136.
80. Филаретов В.В. Схемный подход к символьному анализу активных электрических цепей // Электроника и связь: Науч.-техн. сб.– Киев, 1997.– Вып. 2.– Ч. 1.– С. 97–101.
81. Филаретов В.В. Топологический анализ электронных схем методом выделения параметров // Электричество.– 1998.– № 5.– С. 43–52.
82. Дмитришин Р.В. Кодирование Д-моделей для декомпозиции схем // Электроника и связь.– Киев, 1998.– Вып. 4, ч. 2.– С. 240–244.
83. Dmytryshyn R. D-trees method // Proc. of the 21st seminar on fundamentals of electrotechnics and circuit theory SPETO–98.– Glivece-Ustron, Poland, 1998.– P.347–350.
84. Dmytryshyn R. Hierarchical decomposition of circuit based on d-trees method // Proc. of symbolic methods and applications to circuit design (SMAGD’00).– Lisbon, Portugal.– 2000.– P. 119–124.
85. Филаретов В.В. Метод двоичных векторов для топологического анализа электронных схем по частям //Электричество.–2001.–№8.–C.33–42.
86. Филаретов В.В. Топологический анализ электрических цепей на основе схемного подхода: Дис. … докт. техн. наук: 05.09.05 (Теоретическая электротехника) / Ульяновский государственный технический ун-т и Санкт-Петербургский– С.-Петербург–Ульяновск.– 2002.– 278 с.
87. Защита диссертации В.В.Филаретовым на тему "Топологический анализ электрических цепей на основе схемного подхода": Стенограмма заседания дис. совета Д 212.157.13: Дис. … докт. техн. наук: 05.09.05 (Теоретическая электротехника):– 22 февраля 2002 г.– Протокол № 11.
88. Курганов С.А., Филаретов В.В. Анализ установившихся режимов линейных электрических цепей методом схемных определителей: Учебное пособие.– Ульяновск: УлГТУ, 2002.– 148 с.
89. Курганов С.А., Филаретов В.В. Символьный анализ линейных электронных цепей на основе схемно-алгебраических формул выделения параметров многополюсников // Электричество. – 2003. – № 6. – С. 52–65.
90. Курганов С.А., Филаретов В.В. Символьный анализ и диагностика линейных электрических цепей методом схемных определителей: Учебное пособие.– Ульяновск: УлГТУ, 2003.– 228 с.
91. Курганов С.А., Филаретов В.В. Схемно-алгебраический анализ, диакоптика и диагностика линейных электрических цепей: Учебное пособие.– Ульяновск: УлГТУ, 2005.– 320 с.
92. Королев Ф.А., Курганов С.А., Филаретов В.В. Символьный анализ линейных электрических цепей методом объединения схемно-алгебраических формул // Схемно-алгебраические модели активных электрических цепей: Синтез, анализ, диагностика: Тр. международ. конф. КЛИН–2006. – Ульяновск: УлГТУ, 2006. – Т. 3. – С. 98–115.
93. Шеин Д. В. Ликвидатор избыточных скобок и единиц в сложных алгебраических выражениях // Схемно-алгебраические модели активных электрических цепей: Синтез, анализ, диагностика: Тр. международ. конф. КЛИН–2006. – Ульяновск: УлГТУ, 2006. – Т. 3. – С. 209–213.
94. Волгин Л.И., Корол?в Ф.А., Филаретов В.В. Схемно-алгебраический анализ и топологические преобразования моделей электронных цепей.– Ульяновск: УлГТУ, 2007.– 354 с.
95. Курганов С.А. Особенности объединения подсхем в методах d-деревьев и схемно-алгебраических формул // Синтез, анализ и диагностика электронных цепей: Тр. международ. конф. КЛИН–2007. – Ульяновск: УлГТУ, 2007. – Т. 3. – С. 245–258.
96. Королев Ф. А., Курганов С. А., Филаретов В. В. Сравнение методов анализа электрических цепей по частям в символьном виде // Синтез, анализ и диагностика электронных цепей: Тр. международ. конф. КЛИН–2007. – Ульяновск: УлГТУ, 2007. – Т. 3. – С. 91–104.
97. Королев Ф.А., Курганов С.А., Филаретов В.В. Алгоритм и программа схемно-алгебраического анализа цепей по частям // Синтез, анализ, диагностика электронных цепей: Тр. международ. конф. КЛИН–2007. – Ульяновск: УлГТУ, 2007. – Т. 3. – С. 104–114.
98. Курганов С.А., Филаретов В.В. Неравновесные нуллорные схемы для символьного анализа цепей методом объединения подсхем // Синтез, анализ и диагностика электронных цепей: Международ. сб. науч. тр. САД–2008. – Ульяновск: УлГТУ, 2008. – Вып. 6. – С. 202–210.
99. Курганов С.А., Филаретов В.В. Символьный анализ линейных аналоговых и дискретно-аналоговых электрических цепей.– Ульяновск: УлГТУ, 2008.– 283 с.
100. Королев Ф.А., Филаретов В.В. Иерархический метод матричных нуллорных схем // Электроника и связь (тематич. вып. «Электроника и нанотехнологии»). Ч. 1. – Киев, 2009. – С. 124–129.
101. Королев Ф.А. Сокращение неравновесного нуллорного инварианта для символьного анализа электрических цепей по частям // В настоящем сборнике.
102. Курганов С.А., Филаретов В.В. Нуллорные схемы автономных подсхем // В настоящем сборнике.
103. Rodanski B.S. Symbolic Circuit Analysis: Library of Benchmark Circuits.– http://www.eng.uts.edu.au/~benr/symbolic/
Курганов Сергей Александрович – д.т.н., профессор кафедры «Электроснабжение» Ульяновского государственного технического университета (УлГТУ). 432027, Ульяновск, ул. Северный Венец, 32, УлГТУ; служебный тел. 77-81-05; e-mail: sak@ulstu.ru.
Полях Ольга Игоревна – магистрант радиотехнического факультета Национального технического университета Украины «Киевский политехнический институт (НТУУ «КПИ»), группа РА-41; домашний адрес: г. Киев, ул. Уманская 33а, кв.32; тел. (066) 242 50 95; е-mail: rtf-girl@rambler.ru
Филаретов Владимир Валентинович – д.т.н., профессор кафедры «Электроснабжение» УлГТУ; e-mail: vvfil@mail.ru
Ястребов Николай Игоревич – старший преподаватель кафедры «Теоретические основы радиотехники» НТУУ «КПИ»; e-mail: preptor@mail.ru
|

