СХЕМА СОЕДИНЕНИЙ ЕСТЬ ГРАФ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
И. В. Ерохов
В одной из своих первых работ по теории электрических цепей Г.Кирхгоф применил граф для представления схемы моста постоянного тока [1]. Для студента Кёнигсбергского университета в этом не было ничего необычного, так как в 19-м веке теория графов активно развивалась учеными этого учебного заведения. Таким образом, теория графов участвовала в развитии теории электрических цепей буквально с первых научных работ.
Конечно, Г.Кирхгоф вводил свои понятия, не рискуя переносить терминологию теории графов в работы по электричеству. Схему он называл «системой проводников», узел определял как «точку, в которой сходятся несколько проводников», а контуру дал имя – «замкнутая фигура». Понятие элемента электрической цепи тогда отсутствовало, поэтому роль компонентов схемы выполняли отрезки проводников разного сечения и длины. Может быть, именно это обстоятельство было виною тому, что изображение «системы проводников» не отличалось от современного представления электрической цепи ненаправленным графом.
Описывая предлагаемый метод решения очень сложной «системы проводников», Г.Кирхгоф не отказался от теории графов. Он создал начала первого топологического метода решения [2], ввел понятие «сочетание параметров проводников», не обладающее ни одной «замкнутой фигурой» (дерево схемы). Кроме того, сформулировал понятие коэффициента передачи «сочетания параметров» (произведение значений сопротивлений проводников). Только через несколько десятков лет терминология теории графов войдет в теорию электрических цепей настолько, что ученые этой отрасли знаний заметят: «любой ненаправленный граф может рассматриваться как изображение линейной электрической цепи, параметры ветвей которой равны единице [3]».
Теория графов внесла в теорию электрических цепей мощную методологическую тенденцию, которую принято называть «геометризацией науки». Ее иногда вносят сознательно, чтобы способствовать развитию той или иной отрасли знаний. К понятиям теории графов специалисты теории электрических цепей привыкли настолько, что теория графов выглядит как бесспорное достижение современной теории электрических цепей.
Проиллюстрируем применение некоторых понятий теории графов на простом примере электрической цепи, рис.1, которая хорошо изучена в теории цепей.
В те годы комбинаторными методами занималась и группа научных
работников из Математического института ЧСАН. Результатом этих
исследований была книга «Комбинаторный анализ на практике» [9].
Интересно, что комбинаторный метод анализа также описан в книге [10],
но Кауэр публиковал результаты по этой проблематике в период между
мировыми войнами.
Рис. 1. Изображение лестничной схемы
Схеме рис.1 соответствует ненаправленный граф (именно такого типа граф использован в работе [1]), представленный на рис.2.
Рис. 2. Ненаправленный граф электрической цепи рис.1
Ветвь источника ЭДС на рис.2 не показана, так как его номинал обычно помещают в правой части уравнения (системы уравнений).
В теории графов наряду с графическим изображением используют алгебраическую модель – матрицу смежности (1). Для схемы рис.1 она имеет следующий вид:
Столбцы и строки матрицы (1) соответствуют номерам узлов графа рис.2 –
1, 2, 3, 4, 0.
Известно, что в теории электрических цепей описывают только «независимые» узлы, общий узел исключают как линейно зависимый от остальных и заземляют (или соединяют с точкой известного потенциала). В теории графов поступают аналогично по другим причинам, но в матрице (1) вычеркиваются пятые строка и столбец. Тогда в соответствие с измененной матрицей смежности граф рис.2 значительно упростится, рис.3.
Рис. 3. Разомкнутый путь от узла 1 к узлу 4
Как следует из графа рис.3, лестничная схема может служить моделью разомкнутого пути в графе рис.2 [4].
Кроме матрицы смежности, граф описывают матрицей степеней (валентностей):
Значения элементов главной диагонали матрицы степеней (2) соответствуют числу ветвей, инцидентных каждому узлу. С помощью (1) и (2) получают матрицу полных проводимостей [3]:
Очевидно, что название матрицы (3) взято из теории электрических цепей.
Матрица проводимостей электрической цепи содержится в уравнении, составленном по методу узловых потенциалов. Для электрической цепи рис.1 она имеет вид:
Если значения параметров элементов лестничной схемы будут равны единице, то матрица (4) станет тождественной матрице (3).
В теории графов существует матричная теорема о деревьях:
Если G – мультиграф с вершинами и обозначает число основных деревьев, содержащихся в G, то
где [C]=[D]-[A] - матрица полных проводимостей графа G, а 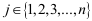 . .
Значение определителя (5) иногда используют как показатель сложности графа G. Некоторые авторы полагают, что эта теорема неявно содержится в классической работе Кирхгофа [1]. Для нашего примера сложность графа рис.2, измеряться величиной –
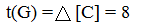 . Детерминант является одним из инвариантов матриц. Приведем все деревья графа рис.2: . Детерминант является одним из инвариантов матриц. Приведем все деревья графа рис.2:
Рис. 4. Деревья графа рис.2
Отметим, что матрица (3) не содержит узла под номером нуль, а в деревьях графа этот узел присутствует.
Из графа рис.2 можно получить еще один подграф, не содержащий контуров. Алгоритм построения такого подграфа Г.Кирхгоф предлагал уже в статье [1]. В нашем случае его легко получить, если «рассечь» общий узел графа рис.5.
Рис.5. Пути передачи сигнала в графе рис.2
Очевидно, что граф рис.5 не является деревом схемы, однако можно заметить, что он повторяет структуру одной из форм Кауэра. Представление входного сопротивления лестничной схемы в виде простой цепной дроби хорошо известно специалистам, поэтому запишем это выражение кратко, как предлагается в источнике [5]:
Лестничная схема чаще всего описывается системой уравнений со смешанным координатным базисом [6]:
Каждая строчка матрицы (7) соответствует некоторому уравнению равновесия. Например, первая строка отражает равновесие ветви, содержащей элемент R1:
Вторая строка – равновесие узла 2:
Вынесем вектор неизвестных из уравнений и получим две первых
строчки матрицы (7):
Продвигаясь дальше по подграфу рис.5, легко составить еще четыре
уравнения равновесия: ветвей – 3, 5 и узлов – 3, 4. Матричная запись
уравнений равновесия образуют систему уравнений (7), которая получена
по подграфу рис.5.
В теории графов придается большое значение поиску замкнутых
путей определенной кратности. Сформулировано несколько теорем, по
которым определяется число таких путей. Это актуально в химии при
исследовании графов сложных молекул, особенно таких, которые
представлены последовательностью простых циклов, где соседние контура
связанны только одним общим ребром, а концевые точки графа связаны
простыми непересекающимися путями.
Общее ребро может занимать одно из двух положений, что показано
на примере двух ячеек графа рис.2.
Рис.6. Разное положение ветви 4, смежной для двух контуров
На рис.6 представлены два варианта расположения ветви 4, которая
является общей для двух контуров: а) ветвь принадлежит контуру с узлами
(0, 2, 3); б) ветвь не принадлежит контуру с узлами (0, 2, 3). Каждый из
вариантов расположения ветви 4 можно изобразить графически так, как
показано на рис.7.
Рис. 7. Разные варианты представления контура (0, 2, 3)
На рис.7,а единичные петли графа представляют собственную
характеристику узлов, их соединяет ветвь. В варианте б) узел 3 не
сохранился, поэтому вторая единичная петля отсутствует.
Каждый из графов рис.7 может быть описан передаточной матрицей
смежности:
Общий коэффициент передачи графа, составленного из двух
контуров, определится следующим образом:
для трех контуров:
При дальнейшем усложнении лестничной схемы, значения элементов
матрицы (9) будут повторять величины элементов ряда Фибоначчи:
Этого следовало ожидать, т.к. структура уравнения производящей
формулы (10) и структура уравнений законов Кирхгофа совпадают,
например:
Уравнения Кирхгофа, приведенные выше, составлены для токов и
напряжений ветвей, о чем свидетельствует индекс b – branch. Как видим,
ток первой ветви определяется на основании токов второй и третьей
ветвей. В отличие от формулы (10) значения величин токов и напряжений
определяются в обратном порядке.
На рис.8 приведена хорошая иллюстрация, взятая из статьи [7]. Как
видим, лестничная схема по праву может быть названа физическим
объектом, представляющим ряд Фибоначчи [8].
Рис. 8. Напряжения и токи ветвей лестничной схемы при единичных параметрах
Важным инвариантом матрицы, представляющей граф, являются
характеристический многочлен 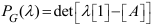 и спектр и спектр 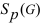 – множество корней многочлена. Графу рис.2 соответствует следующий
характеристический многочлен:
– множество корней многочлена. Графу рис.2 соответствует следующий
характеристический многочлен:
Множество корней многочлена (11), спектр графа Sp(G)
характеризует его свойства [3]. В нашем случае корни будут иметь
следующие значения [9]:
Интересно, что коэффициенты многочлена (11) можно получить,
преобразуя граф рис.2 [3, 10]. Результаты преобразований сведены в
табл.1, где n – число узлов, а ai – значение i-го коэффициента.
Вычисления коэффициентов полинома основаны на выделении
подграфов одновалентного типа
Sp из исходного графа G . Подграфами
Sp являются изолированная ветвь или отдельный контур. Такие подграфы
называются саксовыми графами, их получают из полного графа путем
удаления вершин и ветвей. Например, для третьей строчки таблицы 1
(n = 2) в графе выделены три объекта по одной ветви в каждом, что и
записано во втором столбце. А в последней строке выделен только один
объект с четырьмя узлами – две отдельные ветви. В третьем столбце
можно увидеть процесс вычисления коэффициента многочлена.
Итак, лестничная схема для математиков, изучающих свойства ряда
(10), может служить модельным объектом, т.к. корни характеристического
многочлена (12) повторяют значения, получаемые из ряда Фибоначчи:
Результат (13) получается также из выражения для входного
сопротивления лестничной схемы (6) при условии, что все параметры
ветвей графа равны единице. Такие значения характеризуют особый
случай, а специалистов по теории электрических цепей интересуют
свойства схем с конкретными значениями параметров ветвей.
Получение характеристических многочленов для сложных графов и
нахождение корней является отдельной задачей, которая достаточно
трудна и поэтому не представляет практического интереса для теории
электрических цепей. Наиболее перспективным направлением сегодня
является построение множества путей между заданными точками графа и
математическое описание такого графа, рис.5.
На практике схема соединений электрической схемы участвует в
расчете в виде специальных матриц. Матрицы инциденций являются
алгебраической формой записи схемы соединений элементов цепи, которая
представляется либо как система узлов, либо как система контуров.
Впервые эти матрицы были предложены в работе [1]. В статье Г.Кирхгоф
особо отметил, что элементы матриц принимают значения: 0, –1 и 1 (ток и
напряжение – величины направленные). Очевидно, что матрицы
инциденций составлены для электрической цепи с единичными
параметрами.
1. Кирхгоф Г. О решении уравнений, к которым приводит изучение
линейного распределения гальванических токов // Избранные труды
Г.Кирхгоф. – М.: Наука, 1988. – С. 170 – 178.
2. Ерохов И.В. Реконструкция первого топологического метода
расчета, созданного Г.Кирхгофом // Схемно-алгебраические модели
активных электрических цепей: Синтез, анализ, диагностика: Тр.
международной конф. «Континуальные алгебраические логики,
исчисления и нейроинформатика в науке, технике и экономике (КЛИН –
2006). – Ульяновск: УлГТУ, 2006. – Т. 3. – С. 76 – 83.
3. Цветкович Д., Дуб М., Захс Х. Спектры графов. Теория и
применение. – Киев: Наукова думка, 1984. – 384 с.
3. Цветкович Д., Дуб М., Захс Х. Спектры графов. Теория и
применение. – Киев: Наукова думка, 1984. – 384 с.
5. Хинчин А.Я. Цепные дроби. – М.: Наука, 1978.– 112с
6. Херреро Д., Уиллонер Г. Синтез фильтров.– М.: Сов. Радио, 1971. – 232 с.
7. Владимиров В.Л. Бриллиант Золотого Сечения засверкал
«эффектом бабочки» благодаря исключительному свойству числа Фидия. –
«Академия тринитаризма», М., Эл. № 77-6567, публ. 17119, 19.12.2011.
8. Ерохов И.В. Симметрия объекта, представляющего ряд Фибоначчи.
«Академия тринитаризма», М., Эл. № 77-6567, публ. 17309, 13.02.2012.
9. Ware E. Бесплатное решение алгебраических уравнений 2, 3 и 4
степени // http://www.erichware.com/aktiv/utils/urav234.htm.
10. Полуэмпирические методы расчета электронной структуры// под
ред. Г. Сегал/ пер. с англ. Е.Л. Розенберга. – М.: Мир, 1980. – 164 с.
Ерохов Игорь Васильевич – профессор Запорожского Классического
Приватного Университета (Украина), кандидат технических наук.
E-mail: yerokhov@bigmir.net
|

