ТЕОРЕМА ЗЕЛЯХА–ТЕЛЛЕГЕНА

Введение. В 1951 году в издательстве Академии наук СССР вышла в свет монография [1], которая впервые представляла теорию электрических цепей как отдельную дисциплину. Тираж издания был небольшим (2500 экз.), и книга к настоящему времени стала библиографической редкостью (рис.1). Текст книги был предварен цитатой: «От живого созерцания к абстрактному мышлению и от него к практике – таков диалектический путь познания истины, познания объективной реальности» [2].

Книгу отличает строгое, академическое изложение теории цепей, последовательное использование принципа дуальности к элементам, схемам и сложным математическим выражениям. Это сделало изложение компактным, и вместе с тем более понятным читателю. Но главное достижение монографии – доказательство энергетического баланса схемы, проведенное на максимально высоком уровне абстракции с применением только законов Кирхгофа. Подобные рассуждения, оформленные в виде теоремы, были опубликованы на Западе только в 1952 году [8].

Во введении [1, с. 8] отмечается: «Таким образом, теория линейных электрических схем по своему объему и значению переросла и рамки раздела курса теоретической электротехники. Несомненно, наступила пора рассматривать и развивать теорию схем как самостоятельную дисциплину.». Далее автор указывает на сходство теории схем с геометрией «которая даёт свои законы, абстрагируясь от конкретных предметов, рассматривая предметы, как тела, лишённые конкретности, и определяя отношения между ними никак конкретные отношения каких-то конкретных предметов, а как отношения тел вообще, лишенные всякой конкретности» [3].

Доказательство баланса мощностей схемы. Это доказательство обсуждается в подразделе 1.6. «Баланс мощностей в схеме»[1, с. 36–38]. «В электротехнике широко применяется понятие «мощность». Мгновенной мощностью называют произведение напряжения на ток…».

«С помощью геометрической теории схем можно легко показать справедливость следующего положения, определяющего баланс мощностей в схеме: сумма мгновенных мощностей, доставляемых действующими в схеме источниками, равна сумме мгновенных мощностей, потребляемых или запасаемых остальными элементами схем».

«Для простоты ограничимся доказательством данного положения для схемы, в которой имеются источники лишь одного вида: либо источники напряжения, либо источники тока».

В первом случае пусть каждая из ветвей схемы, как показано на рис. 1.17,а, состоит из последовательно соединенных: источника напряжения E и пассивного элемента, изображенного схематически в виде прямоугольника.

Присоединим мысленно к точкам 1 и 3 сопротивление R = ? для того, чтобы получить замкнутый контур. Тогда для каждой ветви схемы, на основании формулы (1.10,а) {второго закона Кирхгофа – И.Е.}, можно написать равенство

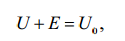
(1.29)

где U – напряжение на крайних узлах ветви, а U0 – напряжение на пассивном элементе.

Соответственно для всей схемы в целом можно написать:

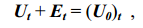
(1.30)

где

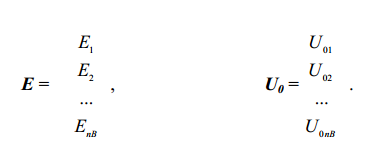
Умножив каждый член равенства (1.30) справа на матрицу Г {матрицу контурных инциденций некоторой схемы – прим. ред.} и учтя (1.26) {U_tГ=0 – второй закон Кирхгофа – прим. ред.}, найдем

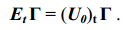
(1.31)

Умножим далее обе части полученного равенства справа на i {вектор контурных токов – прим. ред.} и учтя (1.27) {I=Гi – связь между токами в ветвях и контурными токами – прим. ред.}, придем к равенству

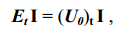
(1.32)

представляющему собой не что иное, как алгебраическую запись положения, справедливость которого и требовалось доказать.

Во втором случае, когда в схеме имеются лишь источники тока, положим, что каждая ветвь состоит из параллельного соединения источника тока и пассивного элемента (рис. 1.17,б)».

Для доказательства баланса мощностей во втором случае воспользуемся принципом дуальности [1, с. 28].

Принцип дуальности. «Если в формулировке любой зависимости между напряжениями и токами электрической схемы провести замену величин и терминов соответствующими дуальными величинами и терминами согласно таблице{R, L, S, u(t), E(t), контур} - {G, C, Г, i(t), J(t), узел}, то новая формулировка сохраняет смысл (хотя и относится уже к другой схеме).

В первоначальной (более узкой) форме этот принцип был известен еще в начале текущего столетия [4].»

Под «формулировкой» в этом положении Э.В.Зеляха следует понимать и сам ход любого доказательства в теории цепей. Таблицу соответствий в обсуждаемом случае следует дополнить новыми терминами {контурные токи, матрица контурных инциденций - узловые напряжения, матрица узловых инциденций} [5]. В результате применения обобщенного принципа дуальности получаем искомое выражение, приведенное в [1, с. 38]

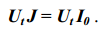
(1.36)

Прежде всего, обратим внимание на введенное понятие «мгновенной мощности». Дело в том, что мощность является удельной величиной и находится как отношение энергии к интервалу времени. Таким образом, мгновенную мощность следует понимать как вектор зафиксированных значений в определенный момент времени. Вектора токов и напряжений также должны представлять собой набор чисел. Однако нигде не сказано, что их значения соответствуют одному и тому же моменту времени. Утверждения (1.32) и (1.36) доказываются только с помощью законов Кирхгофа, закон Ома даже не упоминается. В конце подраздела 1.6 Э.В.Зелях замечает: «Рассмотренное положение вытекает также и из закона сохранения энергии, которому, следовательно, удовлетворяют законы Кирхгофа. Связь между этими законами и законом сохранения энергии рассмотрел впервые (еще в 1886 году) Н.П.Слугинов [6]». Элементарное доказательство теоремы, вытекающее из закона сохранения энергии, приведено в [7]. Таким образом, Элизар Вульфович видел главное в открытии связи между законами Кирхгофа и законом сохранения энергии (что сделано Н.П.Слугиновым), возможно поэтому сформулированное положение не получило в книге [1] статус теоремы.

«Нет пророка в своем Отечестве» и аналогичное положение, сформулированное спустя год Теллегеном [8] получило широкое распространение и развитие в теории электрических цепей под названием «теорема Теллегена» [9,13].

Формулировка Теллегена. Приведем формулировку теоремы из статьи [8] в переводе авторов работы [9].

«Если токи i ветвей цепи произвольной конфигурации и напряжения u – ветвей цепи той же конфигурации таковы, что для любого узла ?i_k = 0 и для любого контура ?u_k = 0, и если для каждой ветви ток направлен от "+" к "-", которые обозначают полярность напряжения этой ветви, то

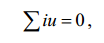
(1)

где суммирование проводится по всем ветвям».

Далее авторы работы [9] показывают, что в монографии [1] доказано то же самое соотношение. Проделаем это вслед за ними. Запишем выражение (1) таким образом, чтобы было видно: напряжения и токи взяты в схеме для различных моментов времени

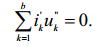
(2)

Убедимся, что матричная форма выражения (2) непосредственно следует из равенства (1.32)

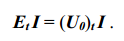
(3)

Действительно, уравнение (3) равносильно уравнению I_tE = I_t(U₀) или I_t{E–U₀} = 0. В фигурных скобках последнего выражения заключен вектор напряжений ветвей. Следовательно, выражение (1.32) (или 1.36) Э.В.Зеляха и выражение (2) Б.Теллегена отображают одно и то же положение, которое с учетом приоритета Э.В.Зеляха следует назвать «теоремой Зеляха–Теллегена».

Следует подчеркнуть, что доказательство Б.Теллегена проведено на уровне уравнений, без использования матричного аппарата линейной алгебры, то есть менее формально, прозрачно и воспроизводимо другими специалистами. Изящное доказательство Э.В.Зеляха предусматривает три этапа: 1) запись уравнений обобщенных ветвей; 2) умножение этого матричного уравнения на матрицу контуров (матрицу узлов) с учетом второго (первого) закона Кирхгофа; 3) умножение полученного матричного уравнения на соответствующий вектор контурных токов (узловых напряжений) с учетом связи между токами в ветвях (напряжениями ветвей) и контурными токами (узловыми напряжениями).

Применение теоремы Зеляха–Теллегена. Покажем вывод теоремы как продолжение рассуждений в монографии [1] . Баланс мощностей электрической схемы находится как одно из произведений:

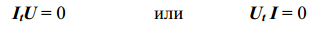
(4)

Раскроем каждое уравнение (4), используя обозначения Э.В.Зеляха:

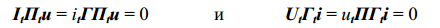
(5)

Из выражений (5) следует равенство, которое является записью теоремы Зеляха–Теллегена в самом абстрактном виде:

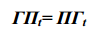
(6)

Тождество (6) используется при получении системы уравнений, составленных по методу переменных состояния. Дело в том, что знаки условно положительных направлений в узле и контуре должны быть согласованы. В статье [10] используется только один знак – для узла, другой знак не устанавливается вообще. Положительный обход контуров может быть разным по направлению, важно только одно, чтобы выполнялось условие (6). Напомним главные этапы этого алгоритма [10].

Выбирается дерево схемы, по которому записывается матрица главных сечений. Матрица сечений преобразуется в фундаментальную матрицу узловых инциденций с одновременным разделением множества ветвей на ветви дерева и ветви связи: П_f=[E F], тогда Г_f=[K E], где E – единичная матрица.

Из тождества (6) следует, что блок K можно найти по формуле:

Таким образом, с помощью теоремы (6) знаки обхода контуров определяются одним условно положительным направлением относительно узла. Другие применения теоремы Зеляха–Теллегена приведены в работах [7, 11].

Обобщение теоремы Зеляха–Теллегена. В работе [11] дается обобщение теоремы в развитие идей монографии [1]. Работу А.М.Иваницкого легко найти в библиотеках, поэтому остановимся на обобщении теоремы из источника [12] . Это надо сделать обязательно, так как авторы статьи развивают идеи Теллегена на Западе. Так ими было описано более 20-ти разновидностей основной теоремы теоретической электротехники [13].

В работе [12] введено понятие оператора Кирхгофа: «Пусть ??- оператор Кирхгофа по току, действие которого по отношению к множеству токов i_? ветвей, принадлежащих цепи из b ветвей, заключается в создании нового множества “токов ?? i_? ” b ветвей, которое подчиняется первому закону Кирхгофа. Пусть также ???- оператор Кирхгофа по напряжению, который может произвести действие над множеством напряжений u_? ветвей, превращая его в новое множество “напряжений ??? u_? ” ветвей, подчиняющихся второму закону Кирхгофа».

Используя введенное понятие, запишем тождество

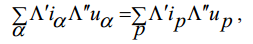
(7)

где i_p, u_p – контурные токи и узловые напряжения, ? ?? ?? , – операторы Кирхгофа, которые могут состоять из последовательности операторов Кирхгофа, примененных в любом порядке, который имеет какой-то смысл.

Элементарными операторами Кирхгофа являются узловая и контурная матрицы инциденций. Соблюдая правила матричных операций, запишем выражение (7) как:

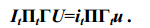
(8)

Левая часть тождества (8) равна нулю согласно законам Кирхгофа, а содержание правой части уточним на примере рис.2.

Графу на рис. 2 соответствуют матрицы инциденций:

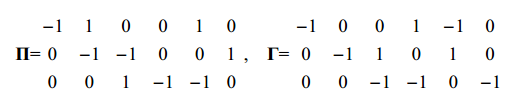
(9)

Произведение вектора контурных токов на матрицу узловых инциденций, уравнение (8), дает следующий результат:

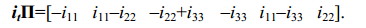
(10)

Последующие два сомножителя позволяют получить вектор-столбец напряжений ветвей:

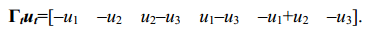
(11)

Выражение (10) представляет собой вектор токов ветвей электрической цепи, граф которой аналогичен рис.2. Вектор (11) содержит напряжения ветвей той же электрической цепи. Этот факт легко проверить по графу электрической цепи рис. 3.

Как видно из примера, выражение (8) справедливо для электрической цепи, граф которой аналогичен рис.2. Таким образом, теорема Зеляха- Теллегена в обобщенной форме (8) сохраняет изначальный смысл.

Заключение. Теорема о псевдомощностях (обобщение теоремы Зеляха–Теллегена) рассматривалась сначала как некоторое соотношение, связывающее данные, измеренные в разные моменты времени на одной и то же схеме. Потом было осознано, что это могут быть разные схемы, объединенные единым графом, другими словами, одной схемой соединения элементов в электрическую цепь.

Интересно ознакомится с формулировкой теоремы, которую приводят в своей работе ученые – последователи Теллегена [12]: «если i'₁,i'₂,...,i'_b являются токами ветвей цепи N? из b ветвей, а u''₁,u''₂,...,u''_b являются напряжениями ветвей другой цепи N?? из b ветвей, где N? и N?? имеют общий линейный граф, однако, могут быть разными, то справедливо следующее равенство:

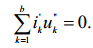
(12)

где суммирование производится по всем ветвям цепи. Правило знаков, принятое для напряжений и токов, таково, что если бы N? и N?? были тождественны, то произведение i'_k u''_k соответствовало бы мгновенной мощности ветви». Как видим, в работе [12] появляется понятие, начиная с которого в монографии [1] строилось доказательство теоремы еще в 1951 году.

Для доказательства справедливости «виртуального» баланса мощностей (12) используются только законы Кирхгофа, что подчеркивает их роль в описании схем. Оказывается, что геометрическая информация о схеме является самой важной составляющей математической модели и с этим непросто согласиться. Закон Ома является самым популярным соотношением у электриков-практиков, а тут он вдруг отходит на второй план. Особенно ярко это следует из выражения для обобщенной формы теоремы Зеляха–Теллегена (8). Следует отметить, что в учебнике [14, с. 61] приведена формулировка теоремы о псевдомощностях, но без доказательства.

1. Теорема Зеляха–Теллегена не только была впервые доказана в нашей стране, но и сама связь между законом сохранения энергии и законами Кирхгофа была открыта нашим соотечественником – Н.П.Слугиновым на шестьдесят пять лет раньше получения результатов Зеляха и Теллегена.

2. Отечественной теории электрических цепей предстоит освоить все формы основной теоремы теоретической электротехники, особенно разностную форму, которая связана с волновым принципом распространения сигнала по электрической цепи. Нам надо наполнить содержанием более сложные операторы Кирхгофа и исследовать их свойства.

3. Теорема Зеляха–Теллегена и ее простое матричное доказательство, предложенное Зеляхом, на наш взгляд, неоправданно не включается в основные учебники по теоретическим основам электротехники и теории электрических цепей, включая последние издания [15, 16]. При этом баланс мощностей в схеме, как правило, излагается без вывода, несмотря на использование в современных курсах узловых и контурных матриц инциденций.

1. Зелях Э.В. Основы общей теории линейных электрических схем. – М.: Изд. АН СССР, 1951. – 336с.

2. В.И.Ленин. Философские тетради.– 1947.– С. 146.

3. Сталин И.В. Марксизм и вопросы языкознания.– Изд-во «Правда».– 1950.– С. 20.

4. Bloch A. On methods for the construction of networks dual to nonplanar networks // Proc. Phys. Soc.– 1946.– 1 nov.

5. Иваницкий А. М. Принцип взаимосоответствия // Радиотехника. – 1976. – Т. 31, № 7. – С. 45–52.

6. Слугинов Н.П. О системе линейных проводников // ЖРФХО: Физ. отд.– 1886.– Т. 18.– С. 177.

7. Ерохов И.В. Энергетический баланс электрических цепей в трудах Г.Кирхгофа // Праці УНДІРТ.– 2006.– № 1.– С. 101–103.

8. Tellegen B.D.H. A general network theorem with applications // Philips Res. Rept.– 1952.– Vol.7 (August).– P. 259–269.

9. Яхинсон Б.И., Иваницкий А.М. О теоремах Зеляха и Теллегена // Радиотехника.– 1973.– Т. 28, № 12.– С.66–67.

10. Stern T.E. On the equation of Nonlinear Networks // IEEE Trans. on circuit theory.– 1966.– CT-13, N 1.– P.74–81.

11. Иваницкий А.М. Обобщение теоремы Теллегена // Радиотехника.– 1974.– T. 29, № 5.– С. 92–94.

12. Penfield P., Spence R., Duinker S. A Generalized Form of Tellegen’s Theorem // IEEE Trans. on circuit theory.– 1970.– CT-17, N 3.– P.302–308.

13. Пенфилд П., Спенс Р., Дюинкер С. Энергетическая теория электрических цепей. – М.: Энергия, 1974. – 152 с.

14. Лосев А.К. Теория линейных электрических цепей: Учебник для вузов. – М.: Высш.шк., 1987. – 512 с.

15. Новгородцев А. Б. 30 лекций по теории электрических цепей. – СПб.: Политехника, 1995. – 519 с.

16. Демирчян К.С., Нейман Л.Р., Коровкин Н.В., Чечурин В.Л. Теоретические основы электротехники: В 3 т. Т. 1.– СПб.: Питер, 2004.– 463 с.

Ерохов Игорь Васильевич – к.т.н., доцент кафедры физической и биомедицинской электроники Запорожского гуманитарного университета «ЗИГМУ» (Украина). E-mail: yerokhov@bigmir.net. Домашний адрес: Украина, 330096, г. Запорожье, ул. Чуйкова, 14А – 73.