ТЕОРЕМА СИГОРСКОГО

Под теоремой В.П.Сигорского здесь понимается теорема об определителе суммы матриц [1].

Теорема. Определитель суммы двух матриц ? и ? порядка m находится по формуле

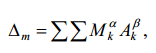(1)

где M^?_k – минор k-го порядка определителя матрицы ?, A^?_k – алгебраическое дополнение (АД) соответствующего минора k-го порядка определителя матрицы ?. В этой формуле ?M^?_kA^?_k – сумма произведений всех возможных миноров и АД соответствующих миноров k-го порядка. Знак A^?_k положителен (отрицателен) при четной (нечетной) сумме номеров строк и столбцов, удаленных для образования этого АД.

В основе выражения (1) лежит понятие алгебраического дополнения минора M порядка k, расположенного в строках с номерами i₁, i₂,…,i_k и столбцах с номерами j₁, j₂,…,j_k некоторой квадратной матрицы ? порядка n

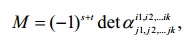(2)

где det?^i1,i2,…ik_j1,j2,…jk – определитель матрицы порядка n–k, полученной из матрицы ? вычеркиванием строк и столбцов минора М; s= i₁+i₂+…+i_k, t= j₁+j₂+…+j_k. Выражение (2) первоначально было использовано в теореме Лапласа о разложении определителя матрицы по некоторому множеству ее строк или столбцов [2]. Теорема Сигорского, как и теорема Лапласа, сводит вычисление определителя n-го порядка к вычислению определителей меньших порядков.

Результат (1) получил широкое применение для формирования полиномиальных схемных функций в символьном и численном виде [3–7]. Однако гораздо менее известно использование теоремы Сигорского в символьном анализе сложных электрических цепей по частям [8–14], чему здесь будет уделено основное внимание.

Первым существенным применением этой выражения (1) было его использование в теоретическом подтверждении достоверности диакоптического метода Д-деревьев [8,9]. Спустя двадцать лет этот проверенный временем результат (1) лег в обоснование диакоптического метода схемных миноров (метода двоичных векторов) [13,14]. При этом было установлено, что разработанные ранее за рубежом метод мультисоединений для анализа по частям графа Коутса [10] и метод нуллорной декомпозиции [11,12] также доказываются и обобщаются с помощью теоремы (1) [14].

Обобщение матричного метода бисекции. Для обоснования большинства символьно-топологических методов использовался и используется матричный подход. Так было и в случае топологического метода бисекции (деление схемы на две части, анализ подсхем в отдельности и объединение результатов анализа подсхем). В случае деления схемы по трем узлам схемная интерпретация теоремы (1) имеет вид где одинарной стрелкой обозначается ориентированный норатор, а сдвоенной – ориентированный нуллатор.

Таким образом, определитель матрицы узловых проводимостей схемы получается через миноры матриц подсхем (левая подсхема описывается матрицей проводимости ?, а правая – матрицей проводимости ?). Базисным узлом (узлом с номером 0)схемы и ее подсхем считается нижний узел. Обозначим верхний и средний внешние узлы подсхем a и b соответственно. Соединение проводником базисного узла с некоторым другим узлом, например узлом a, влечет удаление в матрице соответствующих a-й строки и a-го столбца. Подключение к некоторому узлу a норатора (нуллатора) влечет удаление a-й строки (a-го столбца).

Диакоптическая формула (3) содержит шесть слагаемых, сомножителями в них являются определители матриц проводимостей, которые образованы из матриц проводимостей подсхем путем удаления строк и столбцов, относящихся к общим узлам этих подсхем. Использование матричного метода обусловливает появление дубликаций не только на уровне слагаемых формулы, но и внутри ее сомножителей, что, в частности, затрудняет формирование упрощенных выражений ССФ [15].

Вывод матричной формулы бисекции строится на разложении определителя матрицы по строкам и столбцам (по Лапласу). Это позволяет, хотя и ценой трудоемких выкладок, получать формулы бисекции схемы по четырем и более узлам [11,12]. Вместе с тем в задачах формирования ССФ сложных интегральных схем необходим общий алгоритм построения диакоптических формул для произвольного числа узлов бисекции.

Избежать рутинных выкладок и получить общее решение позволяет обсуждаемая теорема Сигорского, которая, к сожалению, до сих пор не приводится наряду с теоремой Лапласа о разложении определителя по совокупности строк, в учебных курсах по линейной алгебре [http://www.uic.nnov.ru/~znu/algebra/algebra.html] и неизвестна в Дальнем Зарубежье, несмотря на довольно широкую известность в СССР [16].

Структура матрицы схемы, подлежащей бисекции, изображена на рис. 1. Заштрихованные части матриц ? и ?, отображающие подсхемы, содержат параметры элементов этих подсхем. Заштрихованная дважды часть матрицы ?+?, отображающей объединенную схему, находится на пересечении строк и столбцов, соответствующих общим узлам подсхем.

Следует подчеркнуть, что базисный узел схемы здесь и далее считается принадлежащим обеим подсхемам. Сопоставление формулы (1) и рис. 1 показывает, что при нахождении определителя матрицы схемы достаточно учитывать миноры и АД, соответствующие общим узлам подсхем, поскольку остальные миноры и АД равны нулю. Это обусловлено наличием строк и столбцов в матрицах ? и ?, которые состоят из элементов, равных нулю (незаштрихованные части этих матриц на рис. 1).

Значащие (ненулевые) миноры и АД удобно задавать двоичными векторами (ДВ) размерности 2n, где n – число общих узлов подсхем, не считая базисного узла. Первая (вторая) половина ДВ, содержащая n элементов, соответствует строкам (столбцам) матрицы подсхемы ? или ? в заштрихованной дважды части матрицы схемы ?+? (см. рис. 1). Причем удаление строки или столбца отмечается в ДВ единицей. Если данные строка или столбец сохраняются в матрице подсхемы, то это отображается в соответствующей позиции ДВ нулем. Положение или позиции элементов в каждой из половин ДВ задается упорядоченным множеством внешних узлов подсхемы, исключая базисный узел. Обозначениями позиций ДВ служат обозначения узлов схемы.

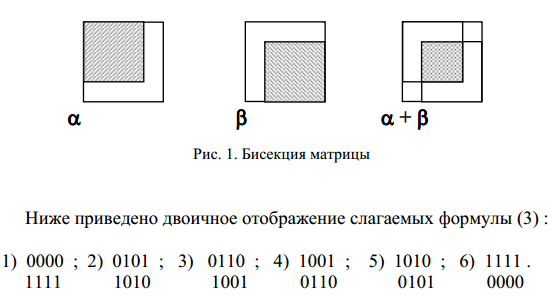Таким образом, слагаемые этой формулы представлены шестью парами ДВ. Векторы каждой пары взаимно дополняют друг друга (как минор и соответствующий минор), отображая сомножители диакоптической формулы. Упорядоченное множество общих (или внешних) узлов подсхем, являющееся обозначением позиций ДВ, имеет вид: (1, 2, 1, 2) или кратко 1212.

В силу одинаковой четности номеров строк и столбцов взаимно дополнительных миноров [16] информацию о знаке слагаемого можно получить из расположения единиц в одном из векторов пары. Принимается во внимание порядковый номер единицы в той или иной половине ДВ. Положительный (отрицательный) знак выбирается в случае четной (нечетной) суммы порядковых номеров позиций, содержащих единицы, в ДВ.

Формирование множества ДВ подсхемы не встречает затруднений. Самое простое решение состоит в том, чтобы перебирать 2n-разрядные двоичные числа (от 2n нулей до 2n единиц) и выбирать те из них, которые содержат одинаковое количество единиц в первой и второй половинах разрядов. Это свойство, вытекающее из формулы (1) и определения ДВ, позволяет получить число ДВ подсхемы в виде

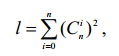(4)

где Cⁱ_n – число сочетаний из n элементов по i.

Имея множество ДВ для одной из подсхем, можно легко получить ДВ второй подсхемы, применив операцию дополнения двоичного числа. Это значит, что единицы в позициях ДВ заменяются нулями и наоборот. Следовательно, общая формула бисекции может быть представлена в виде

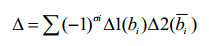(5)

где ?_i – знак i-го слагаемого, определяемый по ДВ b_i, ?1(b_i) – минор, соответствующий b_i, матрицы первой подсхемы; ?2(b_i) – минор, соответствующий дополнению ДВ b_i, матрицы второй подсхемы.

Понятие минора подсхемы и топологический метод бисекции. Формула (5), в отличие от формулы (1), учитывает структуру матрицы схемы, подлежащей бисекции, что исключает рассмотрение слагаемых, у которых один или оба сомножителя равны нулю. Удаление строк и столбцов в матрице наглядно отображается подсоединением нораторов и нуллаторов к соответствующим узлам схемы (3). Это позволяет выполнить бисекцию на схемном уровне и свести раскрытие миноров определителей матриц к разложению определителей нораторно-нуллаторных схем. Однако такие схемы не могут быть проанализированы топологическим методом, поскольку при использовании нуллора утрачивается информация о знаке. Вместе с тем это не мешает применить матричный метод, для которого существенна нумерация узлов схемы [11,12].

С другой стороны, неудаляемый управляемый источник (НУИ) [13,14] обобщает понятие ориентированного нуллора. Следовательно, операция удаления строки и столбца в матрице эквивалентна операции подсоединения НУИ на схеме. При использовании НУИ для анализа схем по частям в понятие ДВ подсхемы вкладывается новое содержание. Единицы в первой (второй) половине элементов ДВ соответствуют конечным узлам подключения генераторов (приемников) НУИ. Базисный узел схемы, который не отражается в ДВ, является начальным узлом всех без исключения генераторов и приемников НУИ.

Для схемной интерпретации формулы (5) по аналогии с минором определителя матрицы подсхемы можно ввести понятие «минор определителя подсхемы» или просто «минор подсхемы». Использование термина «минор подсхемы» более предпочтительно, поскольку этот термин отражает связь топологического метода с матричным методом в отличие от более общего понятия «параметр подсхемы».

Для обозначения миноров схемы или подсхемы может применяться символика, принятая для обозначения миноров матрицы [16]. Нетрудно перейти от обозначений миноров подсхемы с десятичными индексами к ДВ и обратно. Важно, что множество ДВ является унифицированным отображением миноров подсхем с одним и тем же числом узлов. С учетом изложенного выше минор подсхемы, заданный некоторым ДВ, равен определителю схемы, которая получена из этой подсхемы в результате подсоединения НУИ согласно ее ДВ. При использовании матричной бисекции ССФ не зависит от пар нораторов и нуллаторов в нуллорах, то есть любые два норатора и любые два нуллатора могут чередоваться [Bruton]. В отличие от нуллоров НУИ должны быть пронумерованы в соответствии с их очередностью в ДВ, а именно, i-я по порядку единица в первой (второй) половине ДВ соответствует генератору i (приемнику i) i-го НУИ. Все шесть миноров подсхемы с тремя внешними узлами (n=2, l=6) использованы в диакоптической формуле для бисекции схемы по трем узлам

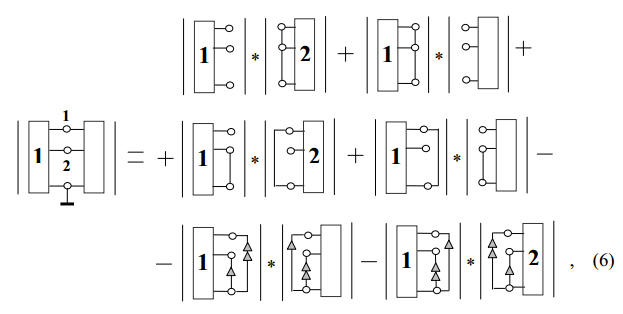В отличие от формулы (5) все сомножители в формуле (6) являются определителями схем, а не матриц. Подобно определителям миноры схемы и матрицы эквивалентны. Однако выражения определителя и миноров матрицы схемы, представленные в развернутом виде, избыточны [14]. Применение схемно-топологического метода выделения параметров [17] позволяет не только избежать построения матриц, но и исключить появление взаимно уничтожающихся слагаемых в выражениях определителя и миноров подсхемы, являющихся сомножителями диакоптических формул. Для нахождения знака слагаемых формулы (6) и ее обобщений может быть использовано, как в формулах (1) и (5), алгебраическое правило, предусматривающее порядковую нумерацию общих узлов подсхем. Однако схема по сравнению с матрицей является топологическим объектом, в котором номера или буквенные обозначения узлов должны служить лишь для указания соединений элементов. Топологическое правило нахождения знака использует ориентацию генераторов и приемников НУИ и не требует сложения номеров узлов и их перенумерации.

Топологическое правило нахождения знака при объединении подсхем. В первую очередь следует объяснить, почему слагаемые формулы (5) при n>1 имеют как положительные, так и отрицательные знаки. Дело в том, что результатом удаления строк и столбцов в матрицах ? и ?, а также последующего сложения этих матриц (см. рис. 1), может быть матрица ?+?, не являющаяся квазидиагональной матрицей [16]. Для того, чтобы представить определитель матрицы ?+? в виде произведения двух сомножителей, каждый из которых содержит элементы только одной из матриц, необходимо выполнить перестановку некоторых строк и столбцов.

Нетрудно убедиться, что число перестановок строк и столбцов, требуемое для такого преобразования матрицы схемы после удаления i-й строки и j-го столбца в матрице ? или ?, находится по формулам соответственно p'=n–i и p''=n–j. Отсюда следует, что сумма i+j оказывает на знак соответствующего слагаемого формулы (5) такое же влияние как сумма p'+p'', поскольку число 2n всегда четное. Преобразования матрицы ? (согласно ДВ) или ? (согласно дополнению ДВ) требуют суммирования p'+p'' для каждой пары номеров строк и столбцов. В силу одинаковой четности номеров строк и столбцов взаимно дополнительных миноров [16] количества перестановок в одной из матриц ? или ? достаточно для приведения матрицы ?+? к квазидиагональному виду. Это доказывает алгебраическое правило нахождения знака, которое используется в формуле (5). Очевидно, именно так рассуждали при получении результата (2), лежащего в основе так называемой «теоремы Лапласа», А.Вандермонд (1771 г.), П.Лаплас (1773 г.) и Э.Безу (1779 г.), но законченное решение сформулировал и доказал О.Коши в 1779 году [2].

С другой стороны, знак слагаемого при классическом разложении определителя матрицы обусловлен четностью числа инверсий в подстановке, образованной номерами строк и столбцов, на пересечении которых находятся выбранные элементы [16]. Следует подчеркнуть, что четность числа инверсий соответствует четности числа перестановок строк и столбцов, необходимого для приведения матрицы этого слагаемого, которая содержит только выбранные элементы, к диагональной форме. Таким образом, вместо установления четности числа перестановок строк и столбцов в матрице ?+?, полученной путем удаления строк и столбцов в матрицах ? и ?, достаточно установить четность числа инверсий в подстановке, первая (вторая) строка которой образована номерами удаленных строк (столбцов). Условимся считать, что формирование подстановки начинается с номеров строк и столбцов, соответствующих матрице ? второй подсхемы.

Нахождение числа инверсий ?_i в подстановке и вычисление знака i-го слагаемого как (–1)^?i было предложено [13] заменить разложением определителя нуллорной схемы, которая образована в результате объединения НУИ, соответствующих ДВ сомножителей этого слагаемого. Для образования нуллорной схемы нумерация НУИ, соответствующих первой подсхеме, должна продолжать нумерацию НУИ второй подсхемы так, что генератор i и приемник i НУИ с номером i занимают i-ю пару из незаполненных очередных позиций в подстановке, образованной генераторами и приемниками. Такое требование вытекает из определения минора подсхемы, для получения которого используется порядковая нумерация подсоединяемых НУИ.

Имеет место изоморфное соответствие между номерами строк (столбцов) и узлами подсоединения генераторов (приемников) НУИ в нуллорной схеме. Как следствие, число инверсий в подстановке, образованной из номеров узлов, равно числу инверсий в подстановке из номеров генераторов и приемников НУИ. Это доказывает топологическое правило, согласно которому определитель нуллорной схемы, равный 1 или –1 в зависимости от четности или нечетности числа инверсий в подстановке, будет соответствовать положительному или отрицательному слагаемому в формуле (5). Используя понятие минора подсхемы, схемный определитель можно найти по топологической формуле

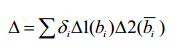(7)

где ?_i – определитель нуллорной схемы, которая образована в результате объединения НУИ, соответствующих ДВ b_i и его дополнению b_i; ?1(b_i) – минор первой подсхемы, соответствующий b_i; ?2(b_i) – минор второй подсхемы, соответствующий b_i.

На основе отображения произвольной квадратной матрицы схемой с источниками тока, управляемыми напряжением [18–20] в [21] было установлено, что «схемные миноры», используемые в диакоптических выражениях (6) и (7), соответствуют не минорам, а алгебраическим дополнениям матрицы. Корректность метода двоичных векторов (схемных миноров) при замене миноров на алгебраические дополнения не нарушается, поскольку сомножители (перемножаемые алгебраические дополнения) имеют одинаковый знак и не влияют на знак соответствующего слагаемого в формуле бисекции.

Метод схемных миноров (схемно-алгебраических дополнений) реализован автором в программе cirsymw, используется в качестве символьного блока системы анализа, диагностики и структурного синтеза SCAD и обеспечивает символьное моделирование схем в десятки–сотни узлов и элементов.

1. Теорема Сигорского (1) является не только эффективным инструментом для символьно-численного моделирования электронных схем, описываемых матрицами, но и математической основой для доказательства методов схемно-алгебраической диакоптики, не требующей использования матричного аппарата.

2. Теорема (1) гармонично дополняет теорему Лапласа, формирует системное мышление для решения сложных задач по частям. Представляется оправданным включение теоремы (1) в учебные курсы по линейной алгебре.

1. Сигорский В.П. Методы анализа электрических схем с многополюсными элементами.– Киев: Изд-во АН УССР, 1958.– 402 с.

2. Математический энциклопедический словарь / Под ред. Ю.В.Прохорова.– М.: Сов. энциклопедия, 1988.– 847 с.

3. Бандман О.Л. Синтез электронных RC-схем. – М.: Наука, 1966.– 247 с.

4. Сигорский В.П., Калниболотский Ю.М. Алгоритмы анализа электронных схем // Изв. вузов. Радиоэлектроника.– 1968.– Т. 11, № 11.– С. 1125–1145.

5. Сигорский В.П. Об одном способе вычисления полиномиальных коэффициентов функций электронной схемы // Теорет. электротехника.– Львов, 1969.– Вып. 6.– С. 41–52.

6. Табарный В.Г., Литвиненко А.А. Программа вычисления коэффициентов полиномов функции электронной схемы // Изв. вузов. Радиоэлектроника.– 1969.– Т. 12, № 8.– С. 787–794.

7. Слипченко В.Г., Табарный В.Г. Машинные алгоритмы и программы моделирования электронных схем.– Киев: Техника, 1976.– 160 с.

8. Дмитришин Р.В., Шаповалов Ю.И. Диакоптический алгоритм анализа сложных линейных цепей на ЭВМ // Автоматизация проектирования в электронике.– Киев, 1975.– Вып. 12.– С. 42–46.

9. Шаповалов Ю.И. Машинный топологический расчет схемных функций электронных схем методом подсхем: Дис. ... канд. техн. наук: 05.13.12 (Системы автоматизированного проектирования и автоматизация технологической подготовки производства в электронной и радиотехнической промышленности) / Львов. политехн. ин-т.– Львов, 1978.– 164 с.

10. Starzyk J. A., Konczykowska A. Flowgraph analysis of large electronic networks // IEEE Transactions on circuits and systems. – 1986. – Vol. CAS- 33, N 3. – P. 302–315.

11. Chang S.M., MacKay J.F., Wierzba G.M. Matrix reduction and numerical approximation during computation techniques for symbolic analog circuit analysis // IEEE Proceedings of the international symposium on circuits and systems (ISCAS).– 1992.– P. 1153–1156.

12. Chang S.M., Wierzba G.M. Circuit level decomposition of networks with nullors for symbolic analysis // IEEE Transactions on circuits and systems.– 1994.– Vol. CAS–41.– P. 699–711.

13. Филаретов В. В. Метод двоичных векторов для топологического анализа электронных схем по частям // Электричество. – 2001. – № 8. – С. 33–42.

14. Филаретов В. В. Топологический анализ электрических цепей на основе схемного подхода: Дис. … докт. техн. наук 05.09.05 (Теоретическая электротехника) / Ульяновский гос. техн. ун-т, Санкт-Петербургский гос. техн. ун-т. – Ульяновск–Санкт–Петербург, 2002. – 265 с.

15. Fernandez F.V., Wambacq P., Gielen G., Rodriguez-Vazquez A., Sansen W. Symbolic analysis of large analog integrated circuits by approximation during expression generation // IEEE Proceedings of the international symposium on circuits and systems (ISCAS).– 1994.– P. 25–28.

16. Сигорский В.П. Математический аппарат инженера.– Киев: Техника, 1977.– 768 с.

17. Филаретов В. В. Топологический анализ электронных схем методом выделения параметров // Электричество. – 1998. – № 5.– С. 43–52.

18. Филаретов В. В. Схемное отображение матрицы для символьного решения систем линейных алгебраических уравнений // Логико- алгебраические методы, модели, прикладные применения: Тр. международ. конф. КЛИН–2001. – Ульяновск: УлГТУ, 2001. – Т. 3. – С. 13–15.

19. Филаретов В. В. О взаимосвязи схемного и матричного определителей // Системы искусственного интеллекта: алгоритмы обработки и модели: Тр. международ. конф. КЛИН–2002. – Ульяновск: УлГТУ, 2002. – Т. 4. – С. 85–93.

20. Павлова Е. А., Филаретов В. В. Схемно-топологическое разложение матричных определителей // Схемно-топологические модели активных электрических цепей: Синтез, анализ, диагностика: Тр. международ. конф. КЛИН–2004. – Ульяновск: УлГТУ, 2004. – Т. 4. – С. 114–119.

21. Павлова Е. А., Серов В. Ф., Филаретов В. В. Выражение K- деревьев через схемные определители и построение безизбыточных формул бисекции электрических цепей // Схемно-алгебраические модели активных электрических цепей: Синтез, анализ, диагностика: Тр. международ. конф. КЛИН–2005. – Ульяновск: УлГТУ, 2005. – Т. 3. – С. 155–173.