ТЕЛЛЕГЕН: ГИРАТОР, НУЛЛОР И ТЕОРЕМА О ВИРТУАЛЬНОМ БАЛАНСЕ
И. В. Ерохов, В. В. Филаретов
Бернард Теллеген родился 24 июня 1900 года в городе Винсхотен
(Winschoten), Голландия. Получил высшее образование в университете
города Делфт (Delft). После окончания учебы в университете с 1923 года
работал в лаборатории фирмы Филипс, город Эйндховен (Philips Research
Laboratories in Eindhoven). В 1926 году ему удалось сконструировать
пентод – вакуумную электронную лампу. Теллеген вводит в теорию
электрических цепей новые идеальные элементы – гиратор (1948т.) и
нуллор (1954г.), а в 1952 году формулирует главную теорему теории цепей
(Tellegen's theorem). В период с 1946 по 1966гг. занимает должность
ассистента профессора теории цепей (adjunct professor of circuit theory) в
университете города Делфт. В 1970 году ему присуждают ученую степень
почетного доктора наук (doctor honoris causa). В 1973 году Теллегена
награждают медалью Эдисона (IEEE Edison Medal). Закончил свой
жизненный путь Бернард Теллеген 30 августа 1990 года и похоронен в
городе Эйндховен.

Бернард Теллеген – Bernard D.H. Tellegen
(24.06.1900 – 30.08.1990)
Гиратор. Рассмотрим вклад ученого в теорию электрических цепей
более подробно и начнем с идеального элемента «гиратор». Конечно, не
только хронология обуславливает такой порядок, лаборатория фирмы
Филипс осуществила репринтное издание оригинальной статьи ученого и
она доступна в Интернет [1]. Ниже мы приводим название работы в
оригинале и выражаем удивление, что репринта статьи 1952 года в архиве
Интернет и библиотеке университета г.Делфт мы не нашли (рис. 1).
Рис. 1. Статья Б.Теллегена «Гиратор – новый элемент электрической цепи»
Определение идеального гиратора даем в соответствие с оригиналом (рис. 2).
Рис. 2. Фрагмент статьи [1].
Б.Теллеген рассматривает трансформатор как четырехполюсник и
записывает уравнения (5) на рис. 2, которые можно получить из А-системы
уравнений четырехполюсника (системы передачи) в предположении
режимов «короткого замыкания» и «холостого хода».
Отметим, что понятие четырехполюсника было введено в 1921 году
Ф.Брайсигом (Franz Breisig) и развивалось многими электротехниками
начала 20-го века, например, Р.Фельдткеллером (Richard Feldtkeller) [2].
Б.Теллеген, без сомнения, знал работы пионеров теории
четырехполюсника, о чем свидетельствует хотя бы ориентация стрелок
токов на входе и выходе (рис.5, вставка) трансформатора. Направление
токов внутрь четырехполюсника теперь является традиционным.
Опишем четырехполюсник с помощью системы уравнений передачи:
где коэффициент Bимеет размерность [Ом ], а коэффициент C – [Ом-1].
Первый коэффициент имеет название «переходное сопротивление»,
второй – «переходная проводимость». Очевидно, что эти коэффициенты
определяют потери в трансформаторе, поэтому у идеального элемента
теории электрических цепей их не должно быть. Тогда система уравнений
(1) получит следующий вид:
Приведем систему уравнений (2) к виду, который она имеет в
оригинальной работе Б.Теллегена:
Достаточно принять условие A ? D и учесть знак тока I2
(четырехполюсник становится «проходным»), и полное соответствие
уравнения (3) с равенствам (5) из оригинальной работы станет очевидным.
Рихард Фельдткеллер (Richard Feldtkeller) приводит схему замещения
четырехполюсника [2], представленную на рис. 3.
Рис.3. Схема замещения четырехполюсника
Как видно из рис. 3, четырехполюсник описан системой уравнений с
применением Z-параметров. Очевидно, что эту схему замещения нельзя
преобразовать в изображение идеального гиратора, так как надо будет
отказаться от всех параметров модели, представленной на рис.2. Теллеген
предлагает другую схему замещения
Рис. 4. Обозначение гиратора, предложенное Б.Теллегеном
нестандартного четырехполюсника. Позднее возникли другие графические
изображения идеального гиратора.
Введенный идеальный элемент теории электрических цепей автор
назвал – «идеальным преобразователем», надо полагать преобразователем
и тока, и напряжения, и энергии. Название получилось громоздким,
поэтому, вероятно, по аналогии с коробкой передач автомобиля, элемент
был назван гиратором, хотя передача момента от двигателя к колесам
автомобиля осуществляется только с потерей энергии. Идеальный статус
гиратора автор подтверждает уравнением [1]:
В обозначениях системы уравнений (1) это равенство будет иметь вид:
Отметим, что преобразования системы уравнений (1) можно
продолжить. Удалять коэффициенты можно не только по два, но и по три,
получая различные идеальные четырехполюсники: 1) источник
напряжения, управляемый напряжением (параметр A); 2) источник
напряжения, управляемый током (параметр B); 3) источник тока,
управляемый напряжением (параметр C); 4) источник тока, управляемый
током (параметр D).
Вернемся к попарному удалению коэффициентов. В системе
уравнений оставим те коэффициенты системы (1), которые были удалены
при получении уравнений (2). В результате такого преобразования
уравнений (1) получается идеальный четырехполюсник, получивший
название конвертора отрицательного сопротивления (КОС):
Комплексные коэффициенты уравнений (5) могут изменять фазу
переменных на любое значение. При разности фаз между током и
напряжением равной значению 1800 получаем идеальный преобразователь
– конвертор отрицательного сопротивления (КОС). Существуют две
разновидности преобразователя – КОСТ и КОСН.
Итак, в любой электрической цепи, преобразующей напряжение
(ток) или энергию сигнала, можно выделить идеальный гиратор. В статье
[1] таким цепям отведен отдельный раздел (рис. 5).
Рис. 5. Начало раздела «Цепи с идеальными гираторами» статьи [1]
Существует преобразование, которое позволяет выделить из матрицы
с комплексными элементами математическое описание реального гиратора
[3]. В своих лекциях профессор Львовского политехнического института
Ю.Т.Величко приводил такой алгоритм:
Пусть матрица комплексных элементов уравнения (6) представляет
линейную модель транзистора (справочники больших фирм-
производителей предоставляют такие коэффициенты).
Тогда в результате преобразования (7) получаем математическое описание
реального гиратора (с частью описания, которое определяет потери). Рис.6
представляет результат преобразования, где идеальный гиратор изображен
в виде полного графа с направленными сторонами, что символизирует
замкнутый контур циркуляции части энергии.
Рис. 6. Представление реального гиратора.
Идеальный гиратор как элемент электрической цепи используется в теории
электрических цепей не только при анализе, но и при синтезе схем.
Аномальный схемный элемент – нуллор. Спектр приложений и
значение нуллора – идеального усилителя Теллегена [4, 5] – отражает
список публикаций из 355 наименований [6]. Этот элемент был введен в
теорию цепей Теллегеном в 1954 году как управляемый источник (УИ),
параметр которого (коэффициент передачи напряжения или передаточная
проводимость) стремится к бесконечности [4]. При этом входное
напряжение и ток УИ становятся равными нулю.
Четырехполюсный элемент нуллор образован двумя аномальными
двухполюсниками: норатором (управляемой ветвью, генератором) и
нуллатором (управляющей ветвью, приемником). Напряжение на нораторе
и ток через него не определены, точнее, определяются схемой, к которой
подключен этот элемент.
Для символьно-топологического анализа электрических цепей Браун
в 1966 году вводит понятие направленного нумерованного нуллора,
отличающееся от классического нуллора Теллегена указанием ориентации
и нумерации. На рис. 7 показаны идеальные операционные усилители и их
замещение ориентированным нуллором.
Ориентированный нуллор позволяет, используя метод выделения
элементов, сформировать определитель схемы и его алгебраические
дополнения без построения уравнений. Для построения схемы числителя
нуллор включается в исходную схему следующим образом: нуллатор
заменяет приемник напряжения или тока, сохраняя их направление, а
норатор подсоединяется взамен источника эдс Е или тока J и
ориентируется противоположно их направлениям. Таким образом,
числители всех передаточных функций для заданных источника и
приемника одинаковы. Эти передаточные функции различаются только
знаменателями – характеристическим полиномом.
Управляемые источники и формулы выделения их параметров. В
практических схемах обычно используются четыре типа управляемых
источников (УИ): 1) источник напряжения, управляемый напряжением
(ИНУН); 2) источник тока, управляемый током (ИТУТ); 3) источник
напряжения, управляемый током (ИНУТ); 4) источник тока, управляемый
напряжением (ИТУН).
В 1996 году В. В. Филаретовым обобщается нуллор Брауна путем
введения понятия ориентированного взвешенного нуллора, названного
неудаляемым управляемым источником (НУИ) [7, 8]. НУИ в отличие от
ориентированного нуллора Брауна имеет параметр ?, который может
принимать любое конечное значение, например равное параметру
выделяемого УИ или единице. В последнем случае взвешенный нуллор –
НУИ становится ориентированным нуллором Брауна.
Определитель схемы получается рекурсивным применением формулы
выделения УИ [8]
где ? – параметр УИ;  (? (?  НУИ) – определитель исходной схемы, в
которой УИ заменен на НУИ, причем генератор УИ – на генератор НУИ, а
приемник УИ – на приемник НУИ; НУИ) – определитель исходной схемы, в
которой УИ заменен на НУИ, причем генератор УИ – на генератор НУИ, а
приемник УИ – на приемник НУИ;  (?=0) – определитель исходной
схемы, в которой нейтрализован УИ. (?=0) – определитель исходной
схемы, в которой нейтрализован УИ.
Схемно-алгебраические выражения (САВ), иллюстрирующие
формулу (8) для различных типов УИ, приводятся в табл. 1. На основе этих
САВ могут быть получены САВ для нахождения схемных функций
соответствующих типов. В этом случае числителем (знаменателем)
схемной функции является первое (второе) слагаемое левой части САВ из
табл. 1. Например, передаточная функция по напряжению находится с
помощью первой строки табл. 1. Благодаря формуле (8), в основе которой
лежит понятие идеального усилителя Теллегена, метод схемных
определителей приобрел самостоятельное значение при решении задач
символьного анализа, диагностики и структурного синтеза электрических
цепей [9].
Таблица 1. Формулы выделения параметров управляемых источников
Теорема Теллегена. В статье [10], увидевшей свет в 1952 году, автор
приводит доказательство общей (general) теоремы теории электрических
цепей, с помощью которой, как он отмечает, можно установить
справедливость уравнения баланса мощностей, теоремы взаимности и
других известных соотношений.
Cтатья [10] начинается с комментария: «Рассуждения, ведущие к этой
теореме, обязательно присутствуют в различных исследованиях цепей, но
сама теорема, насколько это известно автору, никогда не была
сформулирована явно».
Теорема. Пусть в цепи существует множество токов ветвей 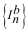 , для
величин которых выполняется уравнение , для
величин которых выполняется уравнение 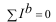 в каждом узле. Пусть
существует также множество напряжений ветвей в каждом узле. Пусть
существует также множество напряжений ветвей 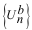 , для величин
которых выполняется уравнение , для величин
которых выполняется уравнение 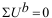 в каждом контуре. Кроме того,
положительное направление для тока ветвей, от (+) к (–), согласовано с
положительным направлением напряжений ветвей, как это показано на
рис.8. Тогда при этих условиях всегда будет справедливо соотношение в каждом контуре. Кроме того,
положительное направление для тока ветвей, от (+) к (–), согласовано с
положительным направлением напряжений ветвей, как это показано на
рис.8. Тогда при этих условиях всегда будет справедливо соотношение
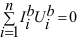 , где суммирование проводится по всем ветвям цепи. , где суммирование проводится по всем ветвям цепи.
Рис. 8. Положительное направление тока и напряжения ветви
Как можно видеть на рис.2, Теллеген предполагал разную
ориентацию стрелки напряжения по отношению к стрелке тока,
т.е. считал обязательным присутствие в цепи ветвей с
источником энергии. Следующие ниже рассуждения представляют
ход доказательства теоремы, приведенный Б.Теллегеном в работе [10].
Доказательство. Обозначим узлы ветви индексами k и l, тогда
напряжение этой ветви находим по формуле 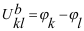 . Ток той же
ветви Ubkl обозначим аналогично напряжению, тогда слагаемое баланса
мощностей запишется следующим образом . Ток той же
ветви Ubkl обозначим аналогично напряжению, тогда слагаемое баланса
мощностей запишется следующим образом
Применим преобразование (9) ко всем ветвям электрической цепи,
тогда слагаемых в выражении 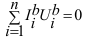 станет в два раза больше.
Сгруппируем слагаемые вокруг каждого из потенциалов узлов цепи,
сомножителем в каждой группе будет сумма токов узла. По первому закону
Кирхгофа эта сумма равна нулю, а, следовательно, баланс мощностей будет
равен нулю. станет в два раза больше.
Сгруппируем слагаемые вокруг каждого из потенциалов узлов цепи,
сомножителем в каждой группе будет сумма токов узла. По первому закону
Кирхгофа эта сумма равна нулю, а, следовательно, баланс мощностей будет
равен нулю.
Как видно, тождество (10) доказано исключительно с помощью законов
Кирхгофа (второй закон Кирхгофа используется в выражении (9)).
Вместе с тем читая формулировку теоремы Теллегена, например, по
источнику [11, 12], невольно сравниваешь ее с определением баланса
электрической цепи, приведенное Э.В.Зеляхом в монографии [13]: «сумма
мгновенных мощностей, доставляемых действующими в схеме
источниками, равна сумме мгновенных мощностей, потребляемых или
запасаемых остальными элементами схем».
Мгновенная мощность включает в себя мгновенные напряжения и
токи (вектора чисел), значения которых соответствуют законам Кирхгофа.
Такие вектора можно определить как для линейных, так и нелинейных
(взаимных и невзаимных) цепей. Отметим, что для схем, представляемых
численными векторами переменных, существует даже вариант принципа
суперпозиции [14].
В общедоступном источнике [15] доказательство теоремы приводится,
именно, со ссылкой на книгу [11], а само доказательство сводится к
краткой записи, которая приводится ниже:
Здесь 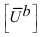 вектор-столбец напряжений ветвей, а вектор-столбец напряжений ветвей, а 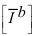 – такой же
вектор токов ветвей. Матрица [A] фиксирует соответствия узел-ветвь, т.е.
является матрицей узловых инциденций, а вектор-столбец – такой же
вектор токов ветвей. Матрица [A] фиксирует соответствия узел-ветвь, т.е.
является матрицей узловых инциденций, а вектор-столбец 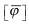 содержит
все потенциалы независимых узлов электрической цепи. Аббревиатура
(KCL) в переводе означает (Кирхгофа-токов-правило). содержит
все потенциалы независимых узлов электрической цепи. Аббревиатура
(KCL) в переводе означает (Кирхгофа-токов-правило).
Ход доказательства в (11) фактически повторяет выкладки Э.В.Зеляха,
приведенные в монографии [13], которая опубликована годом раньше
статьи Б.Теллегена [10]. Однако Э.В.Зелях не сделал последнего шага к
выражению (10), ограничившись записью
Оригинальный результат Теллегена (10) не обременен реальностью в
виде параметров источников и явным родством с законом сохранения
энергии, что непосредственно подвело к понятию «псевдомощность». Это
дало жизнь многочисленным интерпретациям и формулировкам, которые
часто называют «теоремами Теллегена», хотя это обобщения теоремы (10)
[11, 12, 16]. Вокруг ученого создан ореол непререкаемого метра теории
электрических цепей, поэтому многим кажется, что его жизнь проходила в
далеком прошлом. Но это не так, Теллегену просто повезло стать
классиком еще при жизни. Считается, что для классика характерна
некоторая незаконченность высказываний, математических выкладок,
чтобы последователям оставалась возможность приобщиться к его делу.
По-видимому, наиболее точно отражает существо теоремы Теллегена
ее именование «виртуальным балансом сил» [17]. При этом
подчеркивается, что доказательство теоремы Теллегена проводится путем
простого замещения индексов матриц. Понятие «виртуальный» (или
кажущийся) соответствует тому, что токи и напряжения могут быть взяты
как от одной схемы (обычный баланс), так и от различных схем, но
имеющих один и тот же граф (виртуальный баланс). В этом заключается
«отрыв от реальности» – развитие результата, принадлежащего Э.В.Зеляху.
Так, для двух различных электрических схем a и b с l ветвями и
одинаковой структурой может быть составлены следующие виртуальные
балансы:
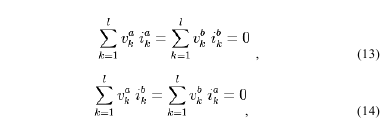
где верхние индексы при напряжениях и токах указывают на их
принадлежность к одной из схем a или b.
Теорема о псевдомощностях (обобщение теоремы Зеляха–Теллегена)
рассматривалась сначала как некоторое соотношение, связывающее
данные, измеренные в разные моменты времени на одной и то же схеме.
Потом было осознано, что это могут быть разные схемы, объединенные
единым графом, другими словами, одной схемой соединения элементов в
электрическую цепь.
Выводы. Бернарду Теллегену было суждено внести неоценимый
вклад в фундамент современной теории электрических цепей. Его научные
результаты в виде идеальных элементов – гиратора и нуллора – составили
основу теории активных электрических цепей. Теллеген, как достойный
преемник Кирхгофа, установил, что геометрическая информация о схеме
является инвариантной составляющей математической модели, поэтому
для доказательства справедливости «виртуального» баланса мощностей
(13) и (14) используются только топологические законы электрического
равновесия и непрерывности. Наследие Теллегена продолжает развиваться
и находить практическое применение в различных областях науки и
техники [6].
1. Tellegen B.D.H. The Gyrator, a new electric network element // Philips
Res. Rept. – 1948. – vol.3.–P. 81–101.
2. Feldtkeller R. Einfьhrung in die Vierpoltheory der elektrischen
Nachrichtentechnik. – Leipzig: Hirzl Verlag, 1948. – 148 s.
3. Величко Ю.Т. Прохідні чотириполюсники. – Київ: Вид.АН УРСР,
1958. – 493 с.
4. Tellegen B.D.H. La recherche pour una s?rie compl?te d’?l?ments de
circuit ideaux non–lin?aires // Rendiconti del seminario matematico e fisico di
Milano: Sotto gli auspice dell’universit? e del politecnico.– Milano, 1955. Vol.
25 (1953–1954).– P. 134–144.
5. Миланцей Т. Идеальный усилитель Теллегена // Синтез, анализ и
диагностика электронных цепей: Тр. международ. конф. КЛИН–2007. –
Ульяновск: УлГТУ, 2007. – Т. 3.– С. 222–234.
6. Kumar P., Senani R. Bibliography on nullors and their applications in
circuit analysis, synthesis and design // Analog integrated circuits and signal
processing.– 2002.– Vol. 33.– P. 65–76.
7. Миланцей Т., Филаретов В.В. От идеального усилителя Теллегена
до многомерного неудаляемого управляемого источника // Схемно-
топологические модели активных электрических цепей: Синтез и анализ:
Тр. международ. конф. КЛИН–2005. – Ульяновск: УлГТУ. – 2005. – Т. 3. –
С. 140–155.
8. Миланцей Т., Славский Г.Н., Филаретов В.В. Пять формул метода
схемных определителей // Схемно-топологические модели активных
электрических цепей: Тр. международ. конф. КЛИН–2004.–Ульяновск:
УлГТУ, 2004.– Т. 4.– С. 102–113.
9. Горшков К.С., Филаретов В.В. Схемный подход Вильгельма
Фойснера и метод схемных определителей / Под ред. В.В.Филаретова.–
Ульяновск: Изд-во УлГТУ, 2009.– 189 с.
10. Tellegen B.D.H. A general network theorem, with application/ Philips
Res. Rept. – 1952. – vol.7, p.p. 259 – 269.
11. Penfild P., Spence R., Duinker S. Tellegen’s Theorem and Electrical
Networks. – Cambridge, Mass.: M.I.T. Press, 1970.– 143 p.
12. Пенфилд П. Энергетическая теория электрических цепей./
П.Пенфилд, Р.Спенс, С.Дюинкер: пер. с англ. – М.: Энергия, 1974. – 152 с.
13. Зелях Э.В. Основы общей теории линейных электрических схем/
Зелях Э.В. – М.: Издание АН СССР. 1951. – 336с.
14. Бондаренко В.М. Вопросы анализа нелинейных цепей. – Киев:
Наукова думка, 1967. – 156 с.
15. Tellegen’s Theorem wikipedia en. / - http://en. wikipedia. org./wiki/
Tellegen’s Theorem.
16. Ерохов И.В., Филаретов В.В. Теорема Зеляха-Теллегена // Синтез,
анализ и диагностика электронных цепей: Международный сборник
научных трудов. – Ульяновск: УлГТУ, 2008. – Вып.6. – С. 6–14.
17. Teorema di Tellegen wikipedia it./ - http://it. wikipedia.
org./Teorema_di_Tellegen.
Ерохов Игорь Васильевич – профессор Запорожского Классического
Приватного Университета (Украина), кандидат технических наук.
E-mail: yerokhov@bigmir.net
Филаретов Владимир Валентинович – д.т.н., профессор кафедры
«Электроснабжение» Ульяновского государственного технического
университета (УлГТУ); e-mail: vvfil@mail.ru
|

