ОТ d-ДЕРЕВЬЕВ К НУЛЛОРНЫМ СХЕМАМ

Простейшие диакоптические формулы. Самыми первыми методами анализа электрических цепей были топологические методы: метод Кирхгофа для – z-схем [1, 2] и метод Максвелла – для y-схем [3, 4]. Развитию диакоптических топологических методов положил начало Фойснер, предложив формулы [5, 6] для определителя схемы, разделенной на две части по одному

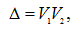(1)

и двум узлам i и j

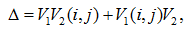(2)

где V₁ и V₂ – определители первой и второй подсхем, V₁(i,j) и V₂(i,j) – определители первой и второй подсхем с объединенными узлами i и j.

Таким образом, понятие подсхемы и формулы (1)–(2) появились задолго до опубликования работ Г.Крона, считающегося основоположником диакоптики [7].

После того как Персиваль ввёл в теорию электрических цепей из теории графов понятие 2-дерева [8], сомножители формулы (1) получили теоретико-графовую интерпретацию: V₁ и V₂ – суммы весов деревьев первой и второй подсхем; V₁(i,j) и V₂(i,j) – суммы весов 2-деревьев первой и второй подсхем соответственно. 2-деревом называют подграф, содержащий две несвязанные между собой компоненты, каждая из которых является деревом. 2-дерево вида – это 2-дерево, в котором вершины i и j находятся в разных компонентах.

Формула для определителя схемы, разделенной на две части по трем узлам i , j и k, была предложена Ю.П.Галямичевым [14–16] где обозначения V₁(i,j), V₂(i,j) со скобками означают суммы весов деревьев определенного типа: (i,j,k) – 3-деревья, в которых все три указанные вершины находятся в различных компонентах; (ij,k), (ik,j), (jk,i) – 2- деревья, в каждом из которых вершины с номерами, указанными до запятой, находятся в одной компоненте, а вершины, приведенные после запятой, находятся в другой компоненте.

Обобщения для активных схем. Персиваль, по-видимому, был первым, кто осознал важность разработки символьного метода для анализа активных электрических цепей. Им были заложены основы двуграфового метода (метода графа тока и напряжения) для y-схем с источниками тока, управляемыми напряжением (ИТУН) [9, 10]. Ю.П.Галямичев заинтересовался возможностью провести анализ таких цепей с помощью поиска деревьев и «неполных» деревьев в пассивной подсхеме после удаления ИТУН [15, 16], применив метод выделения несимметричной части определителя матрицы узловых проводимостей. Например, определитель активной схемы с 2-мя ИТУН находится по формуле

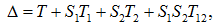(4)

где T,T₁,T₂,T₁₂ – суммы весов определенных k-деревьев; S₁,S₂ – передаточные проводимости первого и второго ИТУН соответственно.

Впоследствии этот метод был развит и формализован в работах Ю.М.Калниболотского и В.С.Рысина [22, 26], В.И.Анисимова и Н.Г.Козьмина [36, 37]. Им удалось обобщить метод выделения параметров активных элементов на схемы, содержащие произвольные трехполюсные управляемые источники (УИ). Для этого используются единичные проводимости для преобразования различных УИ в ИТУН.

Выделение параметров элементы схемы, несмотря на существенно более высокую эффективность по сравнению с перечислением деревьев, входит в противоречие с идеями диакоптики, предусматривающей деление схемы на сравнительно большие подсхемы, а не мелкие части схемы, содержащие ее отдельные элементы. Выделение активных элементов соответствует частному случаю деления схемы на активную и пассивную части. Выбранные таким образом подсхемы имеют слишком много общих узлов и «цена диакоптики» оказывается очень высокой.

Более плодотворной оказалась идея представления как пассивных, так и активных элементов схемы одним графом. Стремительный поиск диакоптического решения задачи символьного анализа электронных цепей вылился в многие сотни статей и десятки монографий.

Штурм обобщений формул (1)–(3). Наибольшее влияние на развитие графовых методов анализа электрических цепей на основе аппарата k-деревьев в дальнейшем оказали приоритетные работы Ботта и Мейбери [11], Робишо и Буавера [12], Мейсона [13] и Чена [19]. В числе зарубежных монографий следует назвать работы Мейсона и Циммермана [17], Робишо, Буавера и Робера [18], а также монографию Чена [31]. Развитие графовых методов в СССР определялось львовскими школами Н.Г.Максимовича [21, 27] и Б.И.Блажкевича [20, 23, 28], а также ленинградской школой В.И.Анисимова [36, 37, 45] (Ленинградский электротехнический институт им. В.И.Ленина).

2- и 3-деревья, а также деревья, содержащие большее число компонент – k-деревья, не вполне точно были названы Ю.П.Галямичевым «неполными деревьями». Правильнее называть неполные деревья или k-деревья термином, известным из теории графов, – «лес деревьев». Точность термина подчеркивается тем обстоятельством, что каждая компонента «леса деревьев» является деревом. Обобщенное понятие k-дерева – это подграф, включающий все узлы исходной схемы (подсхемы) и образованный компонентами связности, каждая из которых является деревом. K-дерево содержит (q – k) ветвей, где q – число узлов исходной схемы (подсхемы). Теоретико-графовые аспекты топологических методов анализа электрических цепей наиболее полно отражены в фундументальных книгах [30, 31].

Для нахождения общего решения требовалось по аналогии с формулами (1)–(3) получить формулы для пассивных цепей, разделенных по 4, 5, …, k полюсам. Формула (3) построена по принципу: если в лесе деревьев первой подсхемы вершины находятся в одной компоненте (дереве), то в лесе деревьев второй подсхемы они должны быть разъединены. 2-деревья (i,j) и 3-деревья (i,j,k) находятся как деревья графа с объединенными узлами i,j и i,j,k соответственно. 2-деревья вида (ij,k) получаются на основе 2-деревьев вида (i,k) или (j,k) выбором 2-деревьев, содержащих путь между вершинами i и j.

Наиболее привлекательной оказалась идея не различать в схеме раздельно пассивные элементы и ИТУН, подобно формуле (4), а учитывать их сходным образом в едином унисторном (двунаправленном [12, 18], корневом [11]) графе [13, 17]. Далее будем использовать термин Мейсона «унисторный граф», чтобы отличать этот вид графа от сигнального графа, дуги которого также имеют направление. Унистором называют однонаправленную проводимость, ток которой пропорционален одному из его узловых напряжений [13]. В общем случае ИТУН заменяется четырьмя унисторами с параметрами, равными по модулю, причем два унистора имеют положительный параметр, а два другие – отрицательный. Каждый двухполюсный компонент – проводимость представляется на унисторном графе двумя встречно направленными дугами с соответствующим весом. Чтобы не загромождать рисунок, двухполюсники можно представлять на графе одним ребром – проводимостью. В этом случае унисторный граф называется комбинированным или смешанным, то есть содержащим как дуги, так и ребра.

Определитель унисторного графа и его составляющие (алгебраические дополнения) находятся с помощью направленных деревьев или прадеревьев. Чаще применяется для этого термин «ордерево», реже «дидерево» – direct tree). Направленным деревом называется дерево, содержащее направленные дуги и корневую вершину, из которой имеются пути во все остальные вершины. При этом в каждую вершину, за исключением корневой, может входить только одна дуга. Из корневой вершины дуги могут только выходить.

Определитель активной схемы с ИТУН, представленной унисторным графом, находится подобно определителю пассивной схемы, и равен сумме всевозможных направленных деревьев [20, 21, 23, 27, 33]

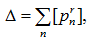(5)

где [p^r_n] – произведение весов дуг, составляющих n-е дерево с корнем в вершине r.

Для направленного графа справедливы формулы нахождения определителя, аналогичные формулам (1)–(3), но с использованием направленных k-деревьев. Направленным k-деревом (направленным лесом) называется k-дерево, состоящее из направленных дуг. Каждая компонента направленного k-дерева является направленным деревом, содержащим свой корень. Направленное k-дерево, как и ненаправленное k-дерево, обладает весом, который равен произведению проводимостей всех его дуг.

Полное множество направленных k-деревьев, построенных для подсхемы и различающихся между собой числом несвязанных компонент, числом вершин в этих компонентах и корневой вершиной в них, полностью характеризуют структурные свойства произвольной подсхемы с n полюсами (внешними узлами). Это множество направленных k-деревьев вместе с их весами составляет структурно-весовое выражение определителя схемы (подсхемы) и его алгебраических дополнений и позволяет использовать эту подсхему как «кирпичик» для добавления к другой подсхеме или подсхемам. Это понимали многие исследователи, однако камнем преткновения оказалась систематизация множества k- деревьев подсхемы в виде ее внешней характеристики, достаточной для объединения этой подсхемы с другими подсхемами.

Задача символьной диакоптики как драма научных судеб. Число работ, посвященных символьно-топологическому анализу электрических цепей по частям было не так велико, попытки решить задачу были, но они не приводили к общему и красивому решению [29, 31, 32, 42, 60, 65, 66].

Недостатком k-деревьев является возрастание их количества по комбинаторному закону при увеличении числа узлов в подсхеме. Советский ученый Р.В.Дмитришин, занимающийся анализом сложных электронных цепей, первым обратил на это внимание и ввел в рассмотрение d-деревья [35], которые строятся только на полюсах (внешних узлах) подсхемы и имеют вид многолучевой звезды. D-деревья позволили «сжать» пространство k-деревьев и сделать его обозримым.

Близкие идеи, почти одновременно с публикациями приоритетных работ [35, 41], высказывал бывший научный руководитель Р.В.Дмитришина – профессор Б.И.Блажкевич с другими учениками, но без формализации метода [40, 44, 46]. Программа [55], в основе которой лежит метод Б.И.Блажкевича и Мочернюка, появилась значительно позже программ серии АС, разработанных Ю.П.Шаповаловым и реализующих метод d-деревьев [41, 43, 48–51]. Это как раз тот случай, когда удачно выбранная интерпретация, способна, как лечь в основу эффективной компьютерной реализации, так и быть воспринятой другими специалистами. Препринт Б.И.Блажкевича и Ю.П.Мочернюка [47], доставленный на защиту диссертации Ю.И.Шаповаловым, не смог сколько-нибудь уменьшить триумф диссертанта и его руководителя.

Наиболее удачно развивалось направление Н.Г.Максимовича, использующее аппарат схемных множеств и деление графа на части по дугам. Я.Н.Матвийчук предложил внешнюю характеристику подсхемы в виде упорядоченных множеств – кортежей вершин – теоретико-множественный аналог d-деревьев [34, 39]. Программы серии ТОПАН, разработанные Я.Н.Матвийчуком [52, 58], как и программы серии АС [59], позволяли получать полиномиальные схемные функции для электронных цепей в десятки узлов и элементов. Программы серии АС и ТОПАН были использованы в промышленности, а программа ТОПАН даже включена в отраслевой стандарт [50] и использовалась на протяжении десятилетий.

Теоретико-множественные построения Я.Н.Матвийчука, унаследованные от Н.Г.Максимовича, затрудняли восприятие диакоптического алгоритма. Н.И.Ястребов, спустя десятилетие после разработки методов d-деревьев и кортежей вершин [63], представил деление графа на части по дугам как частный случай его деления по вершинам и показал единство подходов Р.В.Дмитришина и Я.Н.Матвийчука. С помощью программы PACTOR, в которой Н.И.Ястребов реализовал свою трактовку метода d-деревьев [57, 63, 67], были решены все сложные тесты для программы АС–13ЕС.

Учитывая исследования Н.И.Ястребова, следует отметить, что Р.В.Дмитришин и Я.Н.Матвийчук оказались лидерами в «гонке» символьного анализа электронных цепей по частям. Кроме того, Я.Н.Матвийчуку удалось без посторонней помощи запрограммировать свой алгоритм [39], хотя профессиональная программа Ю.И.Шаповалова отличалась тщательной отработкой основных блоков и реализацией их в машинных кодах (язык Ассемблер) [49].

Группа В.И.Анисимова была близка к разработке подобного диакоптического метода [45]. Для этого В.И.Анисимов и Н.Г.Козьмин использовали внешнюю характеристику подсхемы в виде k-деревьев «путевых видов». Такая работа была начата еще до публикации основной статьи Р.В.Дмитришина и Ю.П.Шаповалова [41], но не вылилась в эффективную программную реализацию.

Направленные d-деревья были переоткрыты на Западе почти на десятилетие позже и названы правильными деревьями (proper trees) [54, 56, 61]. Зарубежным ученым не удалось реализовать конкурентоспособную программу иерархического объединения подсхем [61]. В числе их тестов были многозвенные лестничные структуры, тогда как наиболее популярным советским тестом был избирательный усилитель Лаксберга [38], представленный на рис. 1.

Эффективные программные реализации Я.Н.Матвийчука и Ю.И.Шаповалова показали, что для генерации полиномиальных схемных функций, когда комплексный оператор p учитывается в виде единственной символьной переменной, целесообразно осуществлять наращивание по одной вершине с инцидентными дугами [58] или даже по одному элементу [51, 59]. Первый вид наращивания при анализе схем был предложен еще в 1904 году [5], что подтверждает статус Фойснера как основоположника диакоптики.

Как видно, усилия многих ученых по существу свелись к разработке только одного метода, хотя каждый из них претендовал на разработку своего метода или даже его успешно защитил. Правильно выбранные исходные понятия и математический аппарат определяют успех исследования. Все гениальное – просто. Теперь подробнее о методе Р.В.Дмитришина (рис. 2) или методе d-деревьев [41, 78, 82–84].

Метод d-деревьев (звездных деревьев). D-деревья предназначены, как и k-деревья, для отображения свойств подсхемы с у-ветвями и ИТУН, представленной унисторным графом. D-дерево – это множество изолированных групп полюсов подсхемы (компонент связности), которое отображается кодом, состоящим из соответствующих групп номеров полюсов, разделенных запятыми. Первый полюс в каждой группе является корнем, из него есть путь, содержащий единственную дугу, к любому полюсу данной группы, то есть группа является звездным деревом, центром которого служит корень. Поэтому термин «метод звездных деревьев» лучше бы отражал смысл метода, хотя литера «d» идентифицирует фамилию автора.

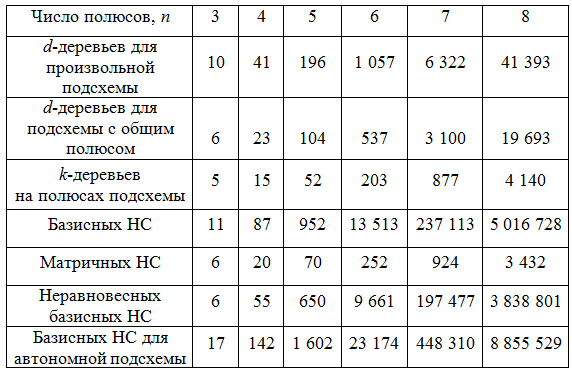
Полное множество d-деревьев, различающихся между собой, подобно k-деревьям, числом изолированных групп полюсов, числом полюсов в этих группах или корневым полюсом в них, характеризует структурные свойства произвольной подсхемы с n полюсами. Число таких деревьев определяется по формуле [41] где 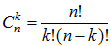. Количество d-деревьев для произвольных подсхем с n = 3…8 приведено во второй строке табл. 1. Число d-деревьев для подсхем с заземленным полюсом дано в третьей строке этой же таблицы.

Таблица 1. Число деревьев и нуллорных схем (НС), характеризующих подсхему

Все d-деревья и их коды для произвольной трехполюсной подсхемы показаны в строках 2 и 3 табл. 2 соответственно. Коды всех 23-х d- деревьев четырехполюсной (полюса обозначены номерами 0, 1, 2 и 3) подсхемы с заземленным полюсом имеют вид:

1 (0123); 2 (1,023); 3 (03,12); 4 (013,2); 5 (03,21); 6 (03,1,2); 7 (012,3); 8 (0,12,3); 9 (01,2,3); 10 (0,21,3); 11 (02,1,3); 12 (0,1,2,3); 13 (0,123); 14 (0,312); 15 (01,32); 16 (01,23); 17 (0,213); 18 (02,13); 19 (02,31); 20 (0,13,2); 21(0,2,31); 22 (0,1,32); 23 (0,1,23),
где жирным курсивом обозначены порядковые номера d-деревьев. Полное множество d-деревьев подсхемы с их весами образует структурно-весовое выражение определителя подсхемы, которое также как и структурно- весовое выражение на основе k-деревьев, позволяет выполнить объединение подсхем.

Таблица 2. D-деревья и их коды для произвольной трехполюсной подсхемы (корневые полюса отмечены знаком +)

Для пассивных цепей d-деревья могут быть преобразованы в неориентированные k-деревья [36], которые построены на полюсах подсхемы. Так, для произвольной трехполюсной подсхемы структурно- весовое выражение определителя, записанное на их основе, имеет вид

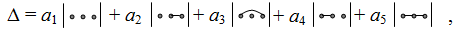(6)

где a₁, a₂, …, a₅ – весовые коэффициенты, содержащие параметры элементов; парой вертикальных линий показан определитель соответствующего k-дерева, который введен по аналогии со схемным определителем [74, 75]. Число ненаправленных k-деревьев приведено в строке 4 табл. 1.

Число d-деревьев для подсхемы можно сократить, учитывая взаимозависимость элементов присоединенной матрицы в соответствии с теоремой Якоби. Например, для объединения трехполюсной подсхемы, имеющей в своем составе полюсы a, b и 0, с другой подсхемой требуется получить для этой подсхемы 6 полиномов (строка 3 и столбец 1 в табл. 1) – определитель подсхемы ?, формируемый при разомкнутых полюсах, и 5 алгебраических дополнений – ?_a,a, ?_b,b, ?_a,b, ?_b,a и ?_aa,bb, где буквы в индексах до или после запятой означают, что в исходной матрице параметров вычеркнуты одноименные строки или столбцы соответственно. Поскольку по теореме Якоби определитель подсхемы

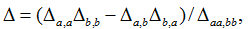(7)

то достаточно найти только 5 полиномов и тем самым сэкономить затраты на поиск соответствующих d-деревьев. Вместе с тем появляются дополнительные затраты на символьные операции в формуле (7) – деление, умножение и вычитание полиномов, в числителе – избыточные взаимно уничтожающиеся слагаемые даже для пассивных цепей с двухполюсными элементами. Таким образом, использование формул вида (7) препятствует реализации преимуществ топологических методов перед матричными методами, для которых характерно наличие взаимно уничтожающихся слагаемых.

Построение структурно-весовых выражений определителей на основе d-деревьев. Нахождение d-деревьев подсхемы и построение их весовых коэффициентов осуществляется путем поиска направленных k-деревьев [33, 53]. Перечисление k-деревьев основано на переборе всевозможных выборок из дуг графа с последующей проверкой путей из заданной корневой вершины во все полюса компоненты. Если в выборке обнаружен контур, то эта выборка сразу отбрасывается. При наличии путей во все узлы каждой компоненты выборка считается k-деревом, а его вес находится путем перемножения проводимостей всех его дуг.

Для каждого полученного k-дерева формируется код соответствующего d-дерева путем проверки путей между полюсами подсхемы. Вес полученного k-дерева добавляется к весу d-дерева с соответствующим кодом. Таким образом находятся все d-деревья и их веса для каждой подсхемы.

Объединение подсхем с использованием структурно-весовых выражений определителей. Объединение подсхем осуществляется путем сочленения каждого d-дерева первой подсхемы с каждым d-деревом второй подсхемы. Полученное соединение двух d-деревьев является направленным k-деревом объединенной подсхемы, если для него выполняются следующие положения: а) во все сочлененные вершины входит только одна дуга; б) вершины, соответствующие внутренним узлам объединенной схемы являются некорневыми; в) нет контуров; г) его вес находится путем перемножения весовых коэффициентов сочленяемых d-деревьев.

d-деревья и их веса для объединенной подсхемы формируются на основе ее направленных k-деревьев следующим образом: а) определяются пути между полюсами объединенной подсхемы, и тем самым формируются компоненты d-дерева; б) если вершина является корневой в обоих сочлененных d-деревьях, то она считается корневой и в d-дереве объединенной подсхемы; если же в сочлененных компонентах корневые вершины разные, то в качестве корня выбирается вершина, в которую не входит дуга; в) вес d-дерева объединенной подсхемы находится путем сложения весов k-деревьев с соответствующим кодом.

Объединение подсхем проводится попарно иерахическим способом по критерию минимальности числа операций. Формулы объединения подсхем зависят только от числа полюсов подсхем, поэтому они могут быть получены для повышения быстродействия алгоритма заранее – до сочленения реальных подсхем [49, 59]. Для получения компактных выражений используются различные приемы группировки слагаемых [51].

Формирование схемной функции на основе структурно-весового выражения схемы. Схемные функции формируются на основе известных зависимостей между алгебраическими дополнениями матрицы узловых проводимостей и весами различных d-деревьев [20, 21, 23, 27, 53]. Так, определитель схемы, симметричное алгебраическое дополнение, несимметричное алгебраическое дополнение, симметричное и несимметричное двойное алгебраическое дополнение находятся по формулам соответственно. В формуле (8) T_?, T_?,i, T_?,ij, T_?,i,j, T_?,i,jk – это суммы весов: деревьев, в которых вершина ? корневая; 2-деревьев, в которых вершины ? и i корневые; 2-деревьев, в которых вершины ?, i корневые и из вершины i есть путь в вершину j; 3-деревьев, в которых вершины ?, i, j корневые; 3-деревьев, в которых вершины ?, i, j корневые и из вершины j есть путь в вершину k, соответственно.

Схемные функции могут быть найдены также путем сочленения схемы с фиктивными подсхемами, обладающими коэффициентами 1, –1, Yн (проводимостью нагрузки), Yг (проводимостью генератора) [59].

Иллюстрация метода d-деревьев. Рассмотрим формирование определителя схемы усилительного каскада на рис. 1,а. Разделим схему на две подсхемы по трем узлам 1, 2 и 3. Активную подсхему – биполярный транзистор – представим на рис. 1,б унисторной схемой замещения с помощью y-параметров [53]. Пассивную подсхему – на рис. 1,в.

Для графа активной подсхемы существует только 9 d-деревьев из 10- ти (строка 2 табл. 1), дерево (21,3) с номером 10 из табл. 2 не существует. Находим эти d-деревья по упомянутому выше алгоритму через k-деревья. Занесем в табл. 3 весовые коэффициенты d-деревьев в виде суммы весов соответствующих k-деревьев. Как видно, в весовом коэффициенте 1-го d- дерева имеется 1 пара, а 3-го d-дерева – три пары взаимно уничтожающихся слагаемых, что является следствием использования избыточной унисторной модели ИТУН.

Аналогично найдем весовые коэффициенты для пассивной четырехполюсной подсхемы с заземленным полюсом (рис. 1,в), для которой максимальное число d-деревьев равно 23 (строка 3 табл. 1), а существует только 12 d-деревьев, веса которых приведены в табл. 4. Остальные 11 d-деревьев отсутствуют, поскольку в графе нет соответствующих путей.

Для объединения подсхем построим таблицу объединения (табл. 5), где в первой строке приведем 9 d-деревьев активной подсхемы, а в первом столбце – 12 d-деревьев пассивной подсхемы. Номера d-деревьев активной и пассивной подсхем в табл. 5 соответствуют их номерам в табл. 3 и 4.

В ячейках на пересечении строк и столбцов табл. 5, соответствующих d-деревьям активной и пассивной подсхем, представим объединенные подграфы, которые проверяются на выполнение условий образования ориентированных k-деревьев.

Всего получается 108 подграфов, из которых свойствам направленных k-деревьев удовлетворяют 46 подграфов, они изображены в табл. 5 (номера узлов подграфа определяются путем сопоставления его с d-деревьями подсхем в этой же таблице). Остальные подграфы не являются k- деревьями и в таблице не приводятся.

Из 46-ти k-деревьев в табл. 5 одиннадцать имеют код d-дерева (0123) и обозначены номером 1 (жирным курсивом) в соответствии с формулой (5). Остальные 35 k-деревьев также помечены номерами соответствующих d-деревьев из той же формулы (5), причем номеру 2 соответствуют 3 k- дерева; 3 – 2; 4 – 3; 5 – 1; 6 – 1; 7 – 2; 8 – 2; 9 – 1; 10 – 1; 11 – 1; 12 – 1; 13 – 3; 14 – 3; 15 – 1; 16 – 1; 17 – 3; 18 – 1; 19 – 1; 20 – 1; 21 – 1; 22 – 1; 23 – 1. D- деревья с номерами 1, 2, …,12, как уже отмечалось, проиллюстрированы в первом столбце табл. 5.

Искомый определитель схемы равен в соответствии с (8) весу d- дерева (0123), которое складывается из весов одиннадцати k-деревьев: где каждой парой чисел обозначено k-дерево, при этом первое число из этой пары – номер соответствующего d-дерева активной, а второе – номер d-дерева пассивной подсхемы. Таким образом, каждая приведенная пара чисел – это координаты ячейки в табл. 5, в которой находится рассматриваемое k-дерево с весом, равным произведению весов соответствующих d-деревьев подсхем.

Приведем выражение определителя, полученное с учетом группировки слагаемых относительно весов d-деревьев пассивной или активной подсхем, общих для группы k-деревьев объединенной схемы с кодом (0123):

В третьей паре скобок формулы (10) имеется два взаимно сокращающихся слагаемых, которые образуются при сложении весов k- деревьев 4–4 и 4–7 из (9), полученные при сочленении d-дерева пассивной подсхемы под номером 4 (в первом столбце табл. 5) с d-деревьями активной подсхемы – с номерами 4 и 7 (из первой строки той же таблицы). Отсюда следует, что метод d-деревьев создает взаимно сокращающиеся слагаемые не только на этапе анализа подсхем, но и на этапе объединения подсхем. Это имеет место, когда d-дерево одной из подсхем образует однотипное объединенное d-дерево с несколькими d-деревьями другой подсхемы, коэффициенты которых содержат параметр одного и того же ИТУН с противоположными знаками.

Устранить взаимно уничтожающиеся слагаемые можно путем использования комбинаторных алгоритмов сортировки слагаемых. Однако это практически невозможно, если при делении схемы на подсхемы унисторы одного ИТУН оказываются в разных подсхемах. Для выполнения этой задачи потребуется получить развернутое выражение всего числителя или знаменателя схемной функции, поэтому необходимо при делении графа на подграфы относить одноименные унисторы к одному подграфу.

Целесообразность использования алгоритмов сортировки слагаемых обусловлена возможностью возникновения значительной аддитивной погрешности (за счет сложения больших чисел с разными знаками) при вычислении весов d-деревьев. Отметим, что погрешность от наличия дубликаций (избыточности выражения) не так сказывается при вычислениях свернутых выражений.

Иерархическое попарное объединение подсхем дает возможность построить схемные функции цепи в виде последовательных выражений с одной операцией деления, что исключает повторяющиеся фрагменты формул, характерные для единых символьных выражений.

Однако, метод d-деревьев обладает существенными недостатками: 1) предназначен для цепей с y-элементами и ИТУН, для анализа цепей, содержащих другие УИ, требуется преобразовать их к ИТУН, что ведет к усложнению схем; 2) генерирует избыточные символьные выражения, которые повышает трудоемкость метода и снижает точность вычислений; 3) использует комбинаторные операции поиска путей в подграфах.

О программной реализации метода d-деревьев (из письма Н.И.Ястребова В.В.Филаретову от 1995 года). «У тебя, наверное, самая большая картотека по символьной тематике. Вот и раскопал Фойснера [6]. Все наши корифеи в своих книгах отталкиваются от Максвелла и Кирхгофа. Честно говоря, у меня тоже всегда была «дурная» привычка докапываться до сути. И она, может быть, помешала мне написать диссертацию. Раскопав суть вопроса, я довольно часто терял к нему интерес, так как убеждался, что вс? это – хорошо забытое старое.

Дам тебе на обкатку свой PACTOP. Внедрите в учебный процесс, если понравится. Да, ещ? забыл. Знакома ли тебе статья Сигорского и Калниболотского [24]? Они в ней пытались систематизировать эти методы. Если будешь писать книгу, то тебе эта статья пригодится.»

Формирование символьных схемных функций. Представленные выше методы диакоптики использовались в 70-е и 80-е годы прошлого века. В то время возможности вычислительной техники были таковы, что задача генерации символьных выражений, когда все параметры схемы представлены в виде символов, не могла быть решена для схем практической сложности в десятки-сотни узлов элементов.

Методы d-деревьев и кортежей вершин изначально не были приспособлены для формирования полностью символьных выражений, поскольку такая задача даже не ставилась. Об этом красноречиво сказал сам Я.Н.Матвийчук [58]. В то же время без свертывания символьных выражений, получаемых при объединении двух подсхем, не обойтись при оптимальной реализации метода d-деревьев для минимизации числа операций [49].

С конца 80-х годов в СССР и России проводятся исследования процесса формирования символьных схемных функций [68–73], разработаны эффективные программы генерации символьных выражений, реализованные Д.В.Шеиным [74–76]. Установленные принципы формирования символьных выражений, позволили получать компактные выражения схемных функций, минуя процесс свертывания [77]. Это позволило получить полное символьное решение [79] для популярной за рубежом тестовой схемы полосового фильтра Старжика и Кончиковской [64, 103], а затем тестовой схемы Лаксберга (рис. 1) [86].

Символьный анализ избирательного усилителя на рис. 1 с помощью реализованной В.В.Филаретовым компьютерной программы CIRSYM (CIRcuit SYMbol) стал возможен только после отказа от использования теории деревьев и разработки нового метода – метода схемных определителей (МСО). МСО базируется исключительно на схемных представлениях, минуя промежуточные модели в виде матриц, графов или теоретико-множественных объектов [80, 81, 85, 86].

Таким образом, предложения, выделенные выше жирным шрифтом (письмо Н.И.Ястребова), в какой-то мере оказались пророческими. Базой для обоснования МСО [86] стал именно метод графа тока и напряжения, предложенный Персивалем [9, 10] и развитый Коутсом [30].

О диакоптике без взаимно уничтожающихся слагаемых. Применение двуграфового метода Персиваля–Коутса и МСО не связано с образованием взаимно уничтожающихся слагаемых – дубликаций, присущих в той или иной степени всем известным методам [68, 71, 72]. Таким образом, использование МСО позволяет избежать дубликаций при анализе подсхем. Однако для объединения подсхем приходится использовать метод двоичных векторов (схемных миноров), в основе которого лежит алгебраическая процедура нахождения знака. Метод двоичных векторов представляет собой схемную интерпретацию теоремы об определителе суммы матриц В.П.Сигорского [24], позволяющую избежать рассмотрения миноров с нулевыми строками и столбцами, но не свободную от образования дубликаций.

Отсутствие в рамках МСО метода объединения подсхем, носящего исключительно схемную природу и свободного от порождения дубликаций, констатировалось во время обсуждения диссертационного доклада В.В.Филаретова [87]. Ниже приводятся выступления участников заседания.

В.В.Филаретов – соискатель: «Методы схемной диакоптики обобщены в работе на случай деления схемы по произвольному числу узлов. При этом количество параметров подсхемы минимально и равно числу слагаемых диакоптических формул. Проведено сравнение разработанных методов с наиболее эффективным для символьно-топологического анализа методом d-деревьев, разработанным Романом Васильевичем Дмитришиным, который здесь у нас присутствует. Например, для задания подсхемы с 10 внешними узлами требуется свыше 1000000 Д-деревьев и всего 48620 миноров. Таким образом, метод d-деревьев оказывается непригодным для деления схем по большому числу узлов. Практически более 7-8 узлов для реализации на современных компьютерах брать нельзя.»

Р.В.Дмитришин (д.т.н., профессор кафедры основ электротехники и информатики Жешувского политехнического института): «Я представляю Жешувский политехнический институт в Польше. Моя фамилия несколько раз здесь повторялась. Я думаю, что несколько предложений мне будет позволительно сказать. С Владимиром Валентиновичем мы знакомы более 15 лет. В то время символьно-топологические методы не были уже популярными. Я с удивлением заметил, что есть еще один чудак, который посвятил свою активную деятельность этой области. Я счастлив, что у Владимира Валентиновича хватило энергии и упорства довести до финала эту работу. И сегодня мы присутствуем на защите такой интересной диссертации. В связи с этим я считаю полезным и историю вспомнить сегодня. Примерно 25 лет назад по указанию сверху топологические методы, символьные методы, были объявлены бесперспективными, ненаучными и т.д. Вдруг исчезли, были закрыты школы профессоров Б.И.Блажкевича, Н.Г.Максимовича во Львове, прекратили существование школы топологического анализа профессора В.И.Анисимова в Ленинграде, профессоров Я.К.Трохименко и Ю.М.Калниболотского в Киеве. Действительно, тяжелое время было... Но интуиция подсказывала, что там все-таки есть рациональное зерно.

В конце я хотел бы сказать, что вот если бы Владимир Валентинович имел возможность выступить на международной конференции по символьным методам... Я уже в двух принимал участие. В Португалии, Лиссабоне и Германии, Кайзерслаутерне. Это было бы ведущее сопротивление. Многие ученые бьются над проблемами генерирования. Это же прикладные задачи. Это же не теория. Сгенерировать короткую формулу, формулу с минимальным количеством арифметических выражений, которые быстрее считаются. Это было бы для России очень представительно. Я считаю, что все, кто может, должны помочь ему в этом. Вот будет осенью в Бухаресте следующая конференция. Вот бы ему выехать и доложиться по основным результатам.»

М.А.Шакиров – научный консультант: «Самое, одно из самых ценных его достижений, заключается в том, что он распространил вот эту методику для активных схем. Это уже параметр любого управляемого источника. Так как их четыре штуки, плакаты все время как-то размножаются. Таким образом, теоретически автор эту проблему закрывает. Причем получает при этом оптимальные выражения, например по длине.

Дальше другой вопрос стоит. А если схемы очень сложные, то как применить эту методику. Автор говорит, что здесь нужно расчленять схему. К сожалению, при этом появляются дубликации. Вопрос об исключении дубликаций в этом случае, когда схема считается методом диакоптики, это, будем так говорить, проблема следующего пятидесятилетия, может быть.»

На разработку искомого метода объединения подсхем – схемно-символьной диакоптики потребовалось в десять раз меньше времени –менее пяти лет. Этот метод, который можно рассматривать как схемно-алгебраическое обобщение метода d-деревьев, обсуждается ниже.

Метод нуллорных схем. Перечисленных недостатков лишен метод нуллорных схем [89, 92, 94–102], использующий непосредственно схему замещения цепи, не содержащую в отличие от унисторного графа избыточных элементов [87]. В этом случае структурно-весовое выражение определителя подсхемы основывается не на d-деревьях, а на нуллорных схемах и называется нуллорно-весовым выражением.

Нуллорной схемой для произвольной линейной неавтономной подсхемы считается схема, содержащая в своем составе только нуллоры и короткозамкнутые ветви, которые эквивалентны параллельному соединению норатора и нуллатора. Поэтому ненаправленные k-деревья в формуле (6) являются также нуллорными схемами. В этом состоит взаимосвязь между d-деревьями и нуллорными схемами.

За основу для построения нуллорно-весовых выражений определителей взяты базисные нуллорные схемы. Базисными называются нуллорные схемы, при перечислении которых не учитываются эквивалентные схемы, получающиеся изменением направления аномальных элементов, заменой параллельного соединения норатора и нуллатора идеальным проводником и переносом норатора (нуллатора) вдоль пути из одноименных элементов [98]. Далее «базисные нуллорные схемы» (там, где это не вызывает недоразумений) будут называться для краткости «нуллорными схемами».

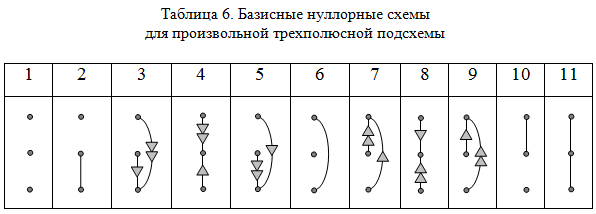
Максимальное число базисных нуллорных схем (верхняя оценка числа нуллорных схем) для произвольной подсхемы с n полюсами определяется как сумма возможных вариантов подключения нуллоров [92]. Для n = 3, 4…8 данные о числе базисных нуллорных схем сведены в строку 5 табл. 1. В табл. 6 приведены все 11 базисных схем для трехполюсной подсхемы. В ячейках 1, 2, 6, 10 и 11 находятся базисные схемы, эквивалентные ненаправленным k-деревьям в формуле (6).

Как видно, максимальное число базисных нуллорных схем больше максимального числа d-деревьев. Однако для реальных подсхем число нуллорных схем в несколько раз меньше их верхней оценки, при этом, чем больше полюсов у подсхемы, тем меньшая доля от соответствующего максимального числа нуллорных схем является ненулевой. Так, для транзистора и четырехполюсной схемы взаимоиндуктивности число нуллорных схем равно шести вместо 11-ти и 87-ми соответственно (строка 4 в табл. 1), для четырехполюсного идеального трансформатора – четырем, для трехполюсного идеального конвертора – двум и т. д. [89]. В результате число нуллорных схем реальной подсхемы часто меньше числа d-деревьев. Так, в приведенном примере число d-деревьев равно 9 и 12 для транзистора и пассивной схемы соответственно, а число нуллорных схем, как видно из последующего рассмотрения, 5 и 10 соответственно.

Построение нуллорно-весовых выражений определителя подсхемы. Нуллорно-весовые выражения находятся путем рекурсивного выделения всех элементов подсхемы при сохранении ее полюсов [89]. Выделение сопротивлений z и проводимостей y осуществляется по формулам Фойснера [5]

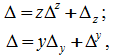(11)       (12)

где ? – определитель схемы; нижний или верхний индексы при символе ? указывают на стягивание или удаление выделяемой ветви соответственно. Стягивание ветви равносильно замене ее идеальным проводником.

Управляемые источники (УИ) выделяются по формуле [81]

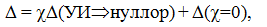(13)

где ? – параметр УИ; ?(УИ⇒нуллор) – определитель исходной схемы, в которой УИ заменен на нуллор, причем генератор УИ – на норатор, а приемник УИ – на нуллатор; ?(?=0) – определитель исходной схемы, в которой нейтрализован УИ.

Формулы выделения параметров не требуют в отличие от алгоритмов построения d-деревьев комбинаторных операций по поиску путей в подграфах. Весовые коэффициенты нуллорно-весовых выражений получаются путем группировки слагаемых перед эквивалентными нуллорными схемами. Эквивалентность нуллорных схем проверяется с помощью отмеченных выше операций.

Нуллорные схемы пассивных подсхем в соответствии с формулами (11) и (12) содержат идеальные проводники. Для трехполюсной подсхемы эти нуллорные схемы приведены в составе нуллорно-весового выражения (6). Для активных цепей нуллорные схемы содержат в соответствии с формулой (13) нораторы и нуллаторы (табл. 6).

Объединение подсхем на основе нуллорных схем. Объединение подсхем, как и в методе d-деревьев, осуществляется попарно иерархическим путем до получения исходной схемы. При этом каждая нуллорная схема первой подсхемы проверяется на совместимость с каждой нуллорной схемой второй подсхемы. Для этого формируется объединенная нуллорная схема с помощью математической операции объединения полюсов и нуллоров обеих нуллорных схем. Если полученная объединенная нуллорная схема не вырождена, то она преобразуется к нуллорной схеме объединенной подсхемы, которая содержит в своем составе только внешние для обеих подсхем полюса. Внутренние полюса оказываются удаленными вместе с последовательными соединениями норатора и нуллатора или объединенными с внешними полюсами, с которыми они соединены идеальными проводниками. При преобразовании объединенной нуллорной схемы к базисной используются уже упомянутые операции изменения направления нуллатора или норатора, преобразования параллельного соединения норатора с нуллатором и переноса нораторов (нуллаторов) вдоль пути из одноименных элементов.

Весовой коэффициент базисной нуллорной схемы объединенной подсхемы равен сумме попарных произведений коэффициентов соответствующих базисных схем объединяемых подсхем. При наличии повторяющихся нуллорных схем их коэффициенты группируются. Множество весовых коэффициентов и соответствующие базисные нуллорные схемы образуют нуллорно-весовое выражение объединенной подсхемы.

В результате нескольких этапов иерархического объединения получается исходная схема со своим нуллорно-весовым выражением. Для получения выражения числителя и знаменателя искомой схемной функции исходная схема объединяется с нуллорными схемами числителя и знаменателя [94] соответственно.

Сокращение числа нуллорных схем. Для многих реальных подсхем можно уменьшить число слагаемых в нуллорно-весовых выражениях, если использовать для их построения матричные нуллорные схемы [100, 101], число которых (строка 6 в табл. 1) значительно меньше числа базисных нуллорных схем (строка 5 в табл. 1).

Матричные нуллорные схемы получаются из множества базисных нуллорных схем путем исключения схем, определители которых могут быть найдены из схемно-алгебраических тождеств [91]. Для трехполюсной подсхемы из одиннадцати базисных нуллорных схем матричными нуллорными схемами являются только шесть – например, с номерами 1, 2, 4, 8, 10 и 11 (табл. 6).