Пример 1. Символьный анализ простейших цепей (делитель напряжения, RC- и LС-фильтры)
Здесь мы рассмотрим примеры символьного анализа нескольких простейших одноконтурных схем.
Вначале вспомним немного теории.
В методе схемных определителей (МСО) искомый отклик цепи (Uвых) представляется в виде отношения двух определителей Uвых=E*ΔN/ΔD. Числитель ΔN здесь является определителем схемы, в которой независимый источник Е и ветвь искомого отклика (Uвых) замещаются нуллором, а знаменатель ΔD – определителем схемы с нейтрализованными входом и выходом.
Формирование определителя выполняется по формуле выделения параметров:
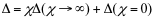
где χi∈{R, g, K, G, H, B}; – определитель первой производной схемы, полученной из исходной схемы в результате присвоения параметру χ значения, стремящегося к бесконечности (сопротивление удаляется, проводимость заменяется на схеме идеальным проводником (стягивается), управляемые источники (УИ) заменяются на нуллоры); Δ(χ=0) – определитель второй производной схемы, которая образовывается в результате нейтрализации выделяемого элемента, то есть, при χ=0 (сопротивление стягивается, проводимость удаляется, УИ нейтрализуется).
1. Расчет делителя напряжения.
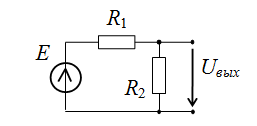
Согласно МСО выходное напряжение рассчитывается по приведенной ниже схемно-алгебраической формуле:
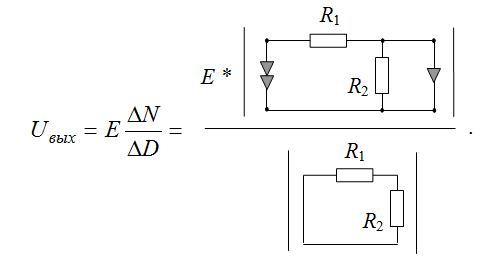
Числитель и знаменатель имеет смысл рассчитывать по отдельности.
Рассмотрим схему числителя.Применяем формулу (1) для выделения параметра сопротивления R2. В результате образуются две новых подсхемы, в первой из которых сопротивление удалено (его параметр стремится к бесконечности, то есть, резистор больше не может пропускать ток и вместо него образуется разрыв), а во второй подсхеме сопротивление заменено идеальным проводником (его параметр становится равным нулю, то есть ток может проходить без потерь).
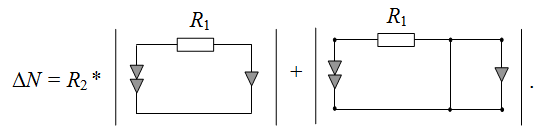
Во второй подсхеме мы видим, что нуллатор (один треугольник) оказался в замкнутом контуре. Это соответствует вырождению схемы, то есть, ее определитель будет тождественно равен нулю (см. Правила вырождения).
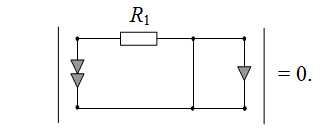
Остается только одна первая подсхема. Попробуем в ней повторить процедуру выделения сопротивления для R1.

Мы видим, что в первой подсхеме при удалении сопротивления элементы нуллора оказались в разрыве, это значит, что определитель подсхемы будет равен нулю (см. Правила вырождения). В результате получаем:
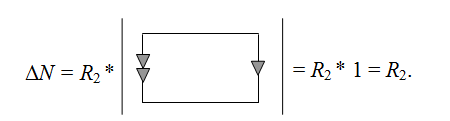
Определитель схемы из контура с нуллором, элементы которого включены встречно, будет равен единице. Таким образом, мы получили значение числителя функции напряжения.
Рассмотрим схему знаменателя.Напомним, что она образована путем нейтрализации входного воздействия. В этом случае источник заменяется на проводник, а выходное напряжение будет равно нулю.
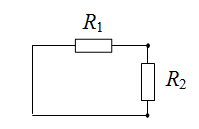
Рассчитываем определитель схемы по формуле (1). Выделяем параметр резистора R2 и получаем две простейшие подсхемы. Их определители известны (см. Простейшие схемы.):
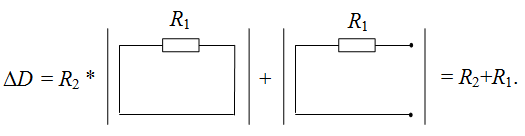
Запишем окончательный результат – классическую формулу для делителя напряжения:
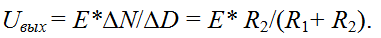
2. Расчет RC-фильтра.
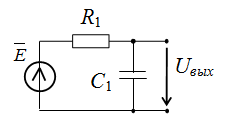
Теперь повторим процедуру расчета для RC-фильтра. Структура схемы идентична структуре делителя напряжения, анализ которого представлен выше. Только источник теперь имеет параметр комплексной эдс , а вместо второго резистора теперь в схему помещен конденсатор. В методе схемных определителей реактивные элементы представляются операторными моделями. Причем параметр емкости удобно рассматривать не в качестве операторного сопротивления, как принято в классической теории цепей, а в качестве операторной проводимости: YC(p) = pC, где р – оператор Лапласа.
Рассмотрим схему числителя.Применяем формулу (1) для выделения параметра операторной проводимости рС1.
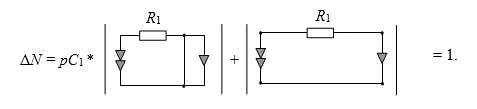
Перейдем к схеме знаменателя.Заменяем источник на проводник, а выходное напряжение становится равным нулю.

После выделения емкостной проводимости мы получили две простейшие подсхемы. Их определители известны (см.Простейшие схемы.). Таким образом, мы получаем выражение для знаменателя: ΔD= pC1R1+1.
Теперь запишем окончательный результат:
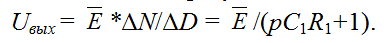
3. Расчет LC-фильтра
Повторим процедуру расчета для схемы LC-фильтра.
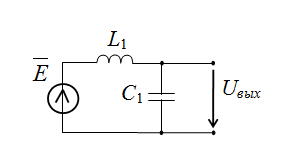
Параметр катушки индуктивности рассматривается как операторное сопротивление катушки: ZL(p) = pL.
Рассмотрим схему числителя.Применяем формулу (1) для выделения параметра операторной проводимости рС1.
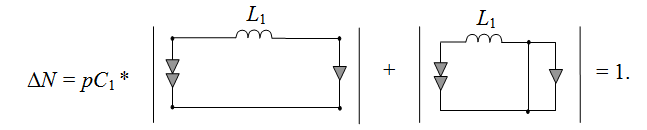
Перейдем к схеме знаменателя.Заменяем источник на проводник, а выходное напряжение становится равным нулю.
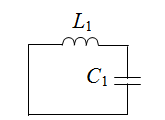
Выделим емкостную проводимость мы получили две простейшие подсхемы. Их определители известны (см. Основы МСО. Простейшие схемы.). Таким образом, мы получаем выражение для знаменателя: ΔD=p2C1L1+1.
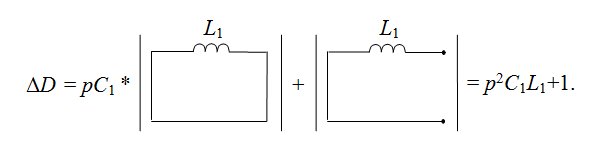
Окончательный результат:
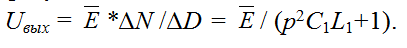
|

