Простейшие схемы

В общем случае рекурсивное выделение параметров из схемы продолжается до тех пор, пока не будет получена простейшая схема, определитель которой выводится из закона Ома. Например, рассмотрим схему с одним сопротивлением

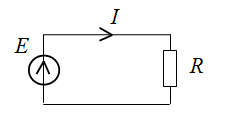
Находим силу тока в цепи:

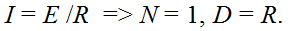
Согласно МСО для нахождения определителя соответствующего числителю схемной функции, в исходной схеме необходимо вместо источника эдс E и тока I поместить норатор и нуллатор соответственно. Применяя формулу выделения параметров получаем две подсхемы:

В первой подсхеме образовался разрыв на участке с идеальным усилителем, следовательно, определитель схемы равен нулю (см. Вырождение). Остается замкнутый контур из норатора и нуллатора направленных встречно. Поскольку из закона Ома следует, что N = 1, то определитель простейшей схемы состоящей из контура с встречно направленными элементами нуллора будет равна единице. В случае согласного направления норатора и нуллатора знак определителя инвертируется.

Для получения знаменателя схемной функции, необходимо нейтрализовать источник напряжения, заменить его проводником, и соответственно обнулить ток в цепи. Получается схема с замкнутым резистором:

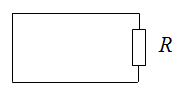
То есть, определитель схемы, состоящей из замкнутого сопротивления равен параметру самого сопротивления.

Теперь рассмотрим другой пример:

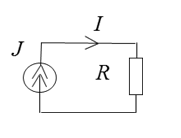
Находим силу тока в цепи:

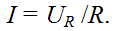
Отсюда напряжение на сопротивлении:

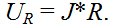
Подставляем в формулу тока, сокращаем, и находим результат, определитель схемы с разомкнутым сопротивлением равно единице:

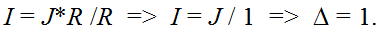
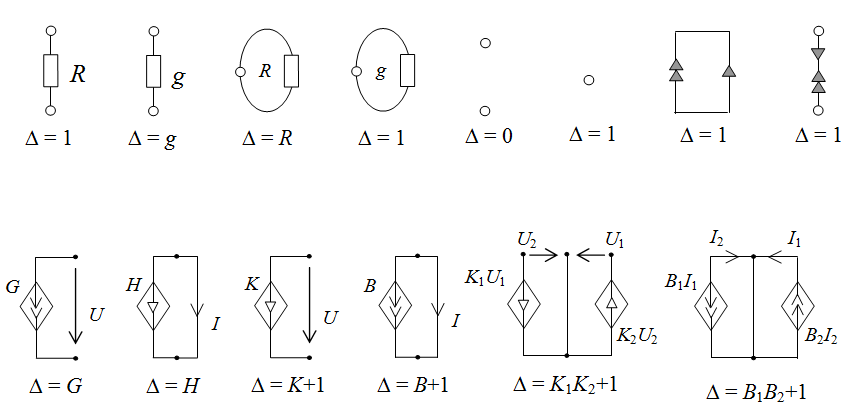
Выполнив аналогичные несложные расчеты для других элементов линейной цепи, можно записать следующие определители для простейших схем: