Пример 3. Разложение определителя полной схемы с помощью бисекции по двум узлам

В этом примере мы применим декомпозиционный подход. То есть, будем при разложении определителя делить схемы на части.

Для любой линейной цепи справедлива формула бисекции по двум узлам, позволяющая разделить исходную структуру на две подсхемы:

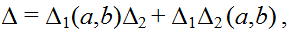
где Δ1 и Δ2 – определители первой и второй подсхем. Обозначение в скобках после Δ указывает на объединение внешних узлов a и b в соответствующих подсхемах.

Выполним расчет определителя полной схемы четвертого порядка (с четыремя узлами).

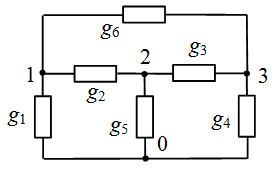
Напомним формулу выделения параметров:

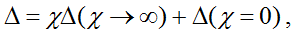
где χ_i∈{R, g, K, G, H, B}; – определитель первой производной схемы, полученной из исходной схемы в результате присвоения параметру χ значения, стремящегося к бесконечности (сопротивление удаляется, проводимость заменяется на схеме идеальным проводником (стягивается), управляемые источники (УИ) заменяются на нуллоры); Δ(χ=0) – определитель второй производной схемы, которая образована в результате нейтрализации выделяемого элемента, то есть принятия χ=0 (сопротивление стягивается, проводимость удаляется, УИ нейтрализуется).

При выделении проводимости g1 образуются две подсхемы Δ (g₁→∞) и Δ (g₁=0), анализ которых целесообразно выполнить по отдельности. В первой подсхеме в результате замены g₁ идеальным проводником проводимости g₂ и g₅ будут соединены параллельно, следовательно, их можно объединить. Если теперь выделить этот элемент с параметром (g₂+g₅), то образуются две простейшие подсхемы (см. Простейшие схемы), определители которых легко выводятся простым сложением или умножением параметров:

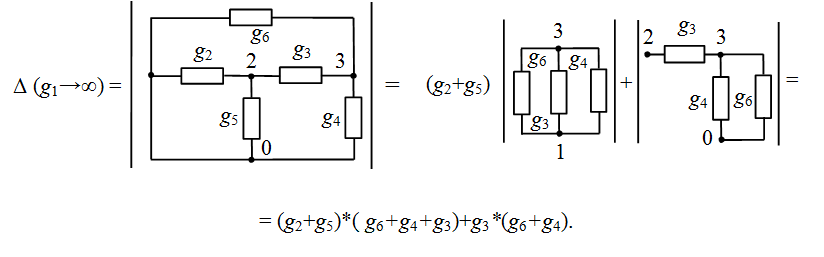
Теперь рассмотрим подсхему Δ (g₁=0), образованную путем удаления элемента g₁. Здесь можно эффективно провести бисекцию по двум узлам с номерами «2» и «3» (на рисунке бисекция обозначена пунктирной линией), с помощью формулы. В результате мы получаем четыре подсхемы, из которых три являются простейшими, и только одна, представляющая из себя контур из проводимостей g₂, g₃ и g₆, требует однократного применения формулы выделения.

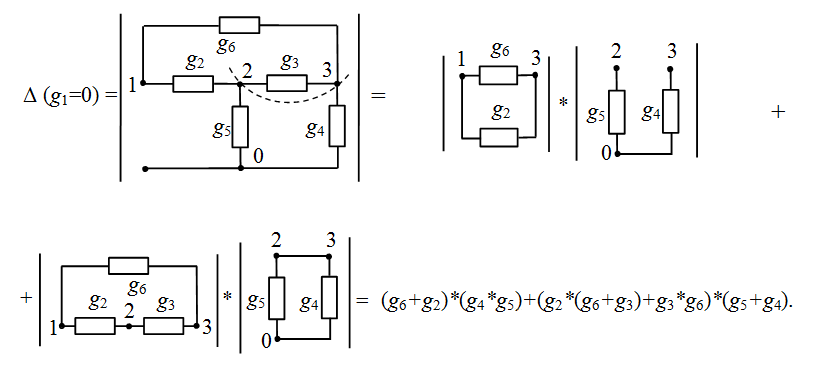
Итого

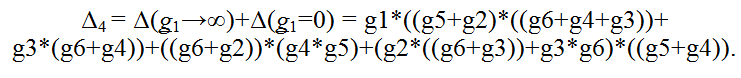
Полученный результат легко проверить, рассчитав определитель матрицы коэффициентов, полученной по классическому методу узловых потенциалов:
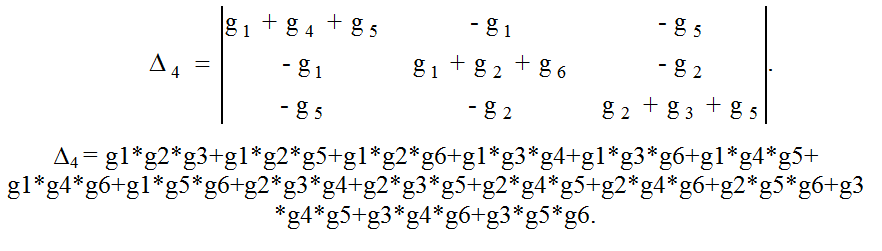