Пример 4. Расчет схем с операционными усилителями
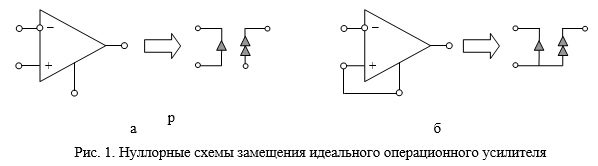
Расчет схем с операционным усилителем (ОУ) во многих случаях удобно выполнять, считая ОУ идеальным. На рис. 1 показаны идеальные операционные усилители и их нуллорные модели.
Для простоты в этом примере мы будем рассматривать схемы только по постоянному току.
1. Расчет инвертирующего усилителя.
Выполним расчет простейшей схемы с ОУ.
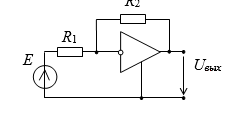
После замены ОУ нуллором схема примет следующий вид:
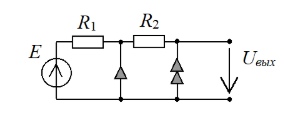
В методе схемных определителей искомый отклик цепи (Uвых) представляется в виде отношения двух определителей Uвых=E*ΔN/ΔD. Числитель ΔN здесь является определителем схемы, в которой независимый источник (Е) и ветвь искомого отклика (Uвых) замещаются нуллором, а знаменатель ΔD – определителем схемы с нейтрализованными входом и выходом.
Напомним, что формирование определителя выполняется по формуле выделения параметров:
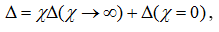
где χi∈{R, g, K, G, H, B}; Δ(x→∞) – определитель первой производной схемы, полученной из исходной схемы в результате присвоения параметру χ значения, стремящегося к бесконечности (сопротивление удаляется, проводимость заменяется на схеме идеальным проводником (стягивается), управляемые источники (УИ) заменяются на нуллоры); Δ(χ=0) – определитель второй производной схемы, которая образована в результате нейтрализации выделяемого элемента, то есть принятия χ=0 (сопротивление стягивается, проводимость удаляется, УИ нейтрализуется).
Расчет схемы числителя.Заменяем источник и ветвь искомого отклика на норатор и нуллатор соответственно. В результате в схеме становится не один, а два нуллора. Их необходимо отличать друг от друга, чтобы использовать правила упрощения схем с нуллорами. Поэтому их элементы помечаются номерными знаками.
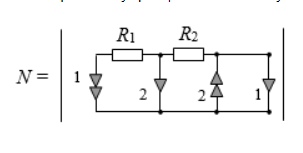
Норатор с индексом 2 и нуллатор с индексом 1 соединены параллельно. Этот контур можно заменить на проводник (см. Простейшие схемы и Нуллор), но для этого требуется объявить их элементами одного нуллора, то есть поменять индексы у пары нораторов или нуллаторов. Важно помнить, что при этом меняется знак у всего схемного определителя. Ниже замена проведена у нораторов: норатор с индексом «1» получил номер «2», норатор с индексом «2» получил номер «1». Аналогичным образом можно было поменять индексы у нуллаторав.
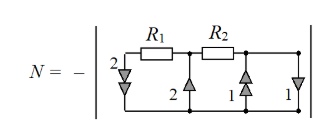
Теперь следует упростить схему. Норатор и нуллатор с индексами «1» направлены согласно, следовательно, в результате их замены на проводник определитель меняет свой знак на противоположный (см. Нуллор):
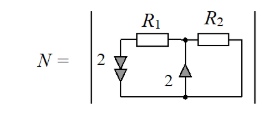
Сопротивление R1 включено последовательно с норатором, в то время как R2 соединено параллельно с нуллатором. Согласно правилам упрощения схем с нуллорами (см. Нуллор), элемент R2 удаляется из схемы, а сопротивление R1 заменяется проводником (закорачивается), а его параметр выносится общим множителем для определителя.
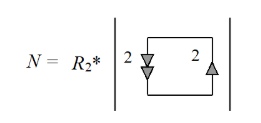
В результате мы получили схему с контуром из норатора и нуллатора включенных встречно. Определитель её равен единице (см. Нуллор). Следовательно числитель схемной функции инвертирующего усилителя:
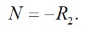
Расчет схемы знаменателя. Нейтрализуем источник и получаем схему с одним нуллором:
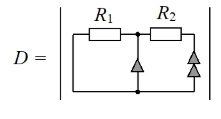
Сопротивление R1 включено параллельно с норатором, в то время как R2 соединено последовательно с нуллатором. Параметр выносится общим множителем и остается схема из контура, состоящего из норатора и нуллатора включенных согласно:
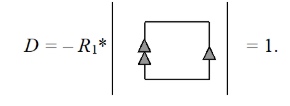
Таким образом, мы получили хорошо известное выражение коэффициента передачи инвертирующего усилителя:
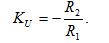
2. Расчет неинвертирующего усилителя
Повторим расчет для неинвертирующего усилителя. Моделируем ОУ с помощь нуллора.
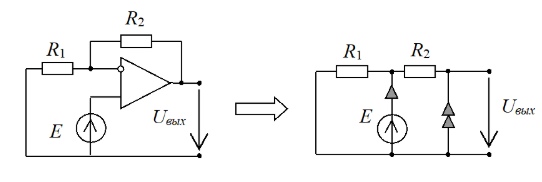
Расчет схемы числителя.Помещаем на вход и выход схемы норатор и нуллатор соответственно. Меняем знаки у элементов нуллора для их сокращения. При этом знак определителя инвертируется.

Расчет схемы знаменателя.Нейтрализуем источник и получаем схему, аналогичную схеме знаменателя в прошлом примере:
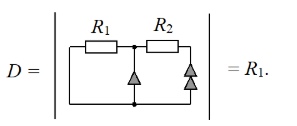
В результате мы получаем классическое выражение коээфициента передачи неинвертирующего усилителя:
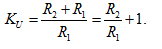
3. Расчет дифференциального усилителя
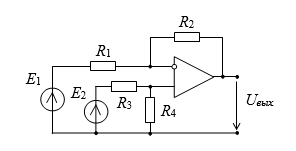
Теперь выполним расчет дифференциального усилителя. Это схема с двумя входными сигналами и одним выходным, поэтому для применения МСО требуется прибегнуть к принципу наложения, согласно которому, отклик цепи с множественными воздействиями, может быть представлен как сумма частичных откликов от каждого воздействия по отдельности. То есть, необходимо отдельно рассмотреть передачу сигнала к выходу от первого источника, потом от второго. Важно отметить, что в обоих случаях знаменатель функции будет одинаковым, так как при его расчете нейтрализуются все источники. Таким образом, требуется получить три схемных определителя:
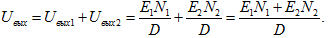
Расчет схемы числителя N1.Нейтрализуем источник Е2. Помещаем норатор вместо Е1 и нуллатор на выход схемы. Меняем знаки у элементов нуллора и упрощаем схему в соответствии с правилами:
Расчет схемы числителя N2.По аналогии выполняем расчет схемы числителя, при передачи сигнала с источника Е2 на выход дифференциального усилителя:

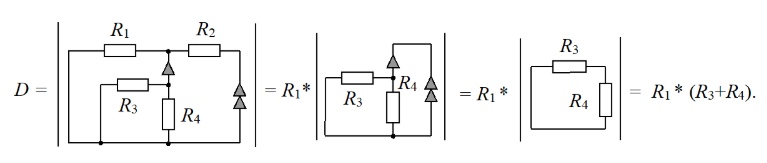
Расчет схемы знаменателя.Нейтрализуем источник и получаем схему, с одним нуллором. Выполняем эквивалентные упрощения и получаем выражение схемного определителя:
Подставляем полученные результаты в общую формулу и получаем функцию выходного напряжения дифференциального усилителя:
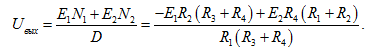
|

