Пример 5. Расчет схем с управляемыми источниками

В этом разделе мы обсудим применение МСО для расчета схем замещения электрических цепей, в которых присутствуют управляемые источники (УИ). Параметры управляемых источников выделяются по той же формуле, что и параметры пассивных элементов:

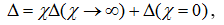
где χi∈{R, g, K, G, H, B}; – определитель первой производной схемы, полученной из исходной схемы в результате присвоения параметру χ значения, стремящегося к бесконечности (сопротивление удаляется, проводимость заменяется на схеме идеальным проводником (стягивается), УИ заменяются на нуллоры); Δ(χ=0) – определитель второй производной схемы, которая образовывается в результате нейтрализации выделяемого элемента, то есть, при χ=0 (сопротивление стягивается, проводимость удаляется, УИ нейтрализуется).

1. Расчет схемы с неидеальным ОУ.

В случае если в схеме с ОУ требуется учесть конечный коэффициент усиления, то вместо нуллора часто используется источник напряжения, управляемый напряжением (ИНУН). Рассмотрим анализ схемы с ИТУН, представленной ниже:

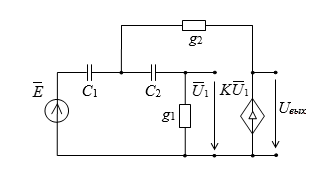
Расчет схемы числителя.В схеме соответствующей числителю передаточной функции параметр емкости рС1 может быть сразу вынесен за скобку, так как она включена последовательно с норатором:

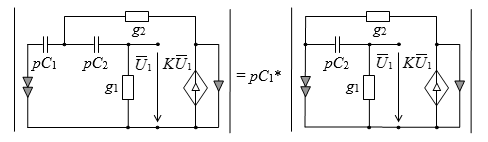
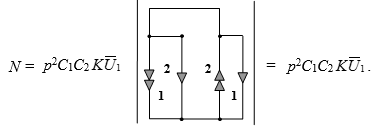
Если теперь применить формулу (1) для выделения параметра ИТУН, то мы получаем две новых подсхемы:

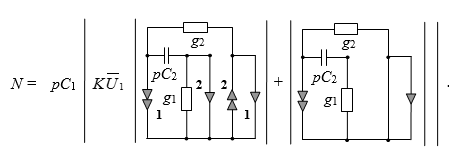
Следует отметить, что вторая подсхема оказалась вырожденной, поскольку в ней образовалась закоротка с нуллатором. То есть, при параллельном соединении управляемого источника напряжения с элементами нуллора, параметр УИ выносится за скобку, а сам ИНУН заменяется на новый нуллор. В то же время, первая подсхема легко упрощается в соответствии с правилами (см. Нуллор):

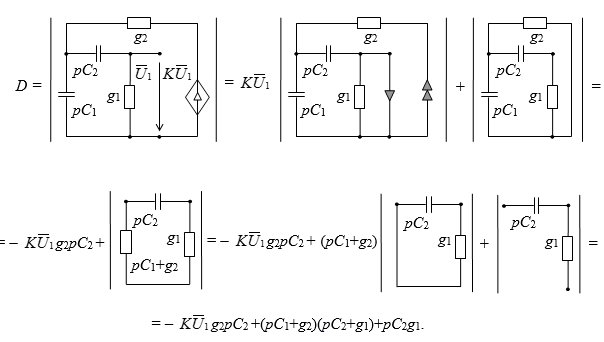
Расчет схемы знаменателя. Выделяем параметр управляемого источника, получаем две подсхемы, первая из которых легко упрощается. Во второй подсхеме выделяем параллельно соединенные проводимости pC1 и g2, предварительно объединив их в один элемент:

В результате мы получаем символьную функцию:

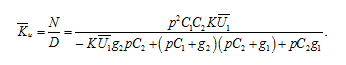
2. Расчет схемы с взаимной индуктивностью

Схемы, включающие в себя индуктивно связанные катушки, можно рассчитывать с помощью МСО, если магнитную связь между катушками моделируется с помощью источников напряжения управляемых током (ИНУТ). Так, рассмотрим простую схему, в которой связанные катушки находятся в разных контурах:

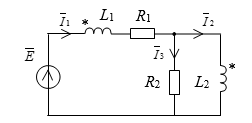
Составляем систему уравнений по законам Кирхгофа:

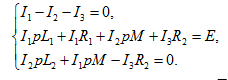
Здесь параметр М – взаимная индуктивность, ZM = рМ – операторное сопротивление взаимной индуктивности. Величина UM = IpM соответствует напряжению взаимной индуктивности на одной из связанных катушек. Это напряжение зависит от тока, протекающего через вторую катушку, то есть мы имеем дело с источником напряжения, управляемым током. Поскольку параметр H=U/I соответствует сопротивлению, то если принять H=pM, то можно составить следующую схему замещения:

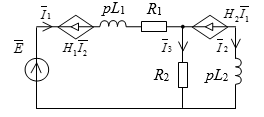
Выполним расчет тока I3 в этой схеме.

Расчет схемы числителя. После замены источника и тока на норатор и нуллатор параметр сопротивления R2 можно сразу удалить:

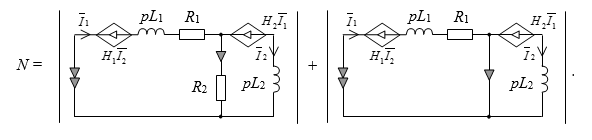
Если теперь выделить по формуле (1) параметр первого ИТУН, то мы получим подсхему с последовательным соединением двух нораторов, что приводит к её вырождению:

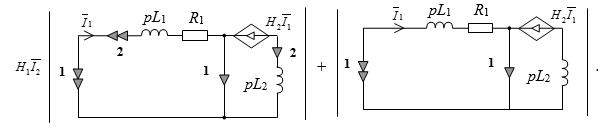
Из подсхемы выделяем параметр второго ИТУН, и после сокращения получаем выражение для числителя:

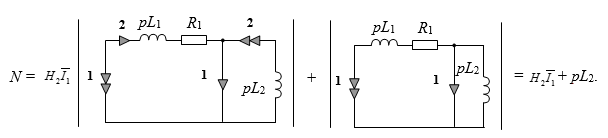
Расчет схемы знаменателя. В схеме знаменателя выделяем параметр первого ИТУН, получаем выражения вида:

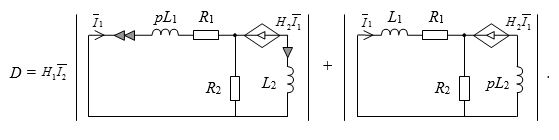
Для удобства выполняем расчет подсхем по отдельности:

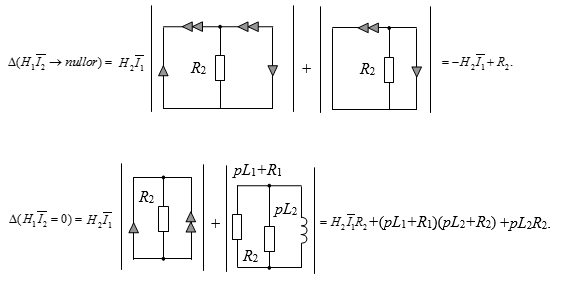
Наконец, запишем окончательный результат:

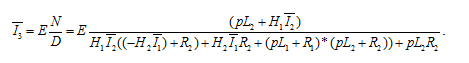
Расчет системы уравнений по законам Кирхгофа приведет к аналогичному символьному выражению.